Lab 8: Genetic Algorithms
Due November 12 by midnight

Starting point code

Use Teammaker to form your team. You can log in to that site to indicate your partner preference. Once you and your partner have specified each other, a GitHub repository will be created for your team.

Introduction

The objectives of this lab are to:

• Understand the details of how a standard genetic algorithm operates.
• See how to specialize the genetic algorithm to evolve neural network weights.
• Apply the neural genetic algoirthm to solve reinforcement learning problems in a new way.

The main steps of this lab are:

• Implement the class GeneticAlgorithm with chromosomes of bits.
• Implement the class NeuralGA, which is a specialization of class GeneticAlgorithm, with chromosomes that represent the weights and biases of a fixed neural network architecture.
• Implement the class RLNeuralGA, which is a specialization of class NeuralGA to solve reinforcement learning problems.

You will modify the following files:

• ga.py
• sum_ga.py
• neural_ga.py
• rl_neural_ga.py

You will use, but not modify, our implementation of neural networks from Lab 5, which is called neural_net.py. The Network class has been updated with two additional methods getWeights() and setWeights() to facilitate using neural networks within a genetic algorithm.

Implement the GeneticAlgorithm class

Open the file ga.py. You have been given a skeleton definition of the GeneticAlgorithm class that you will complete. Read through the methods that you will need to implement. Notice that the last two methods, called fitness and isDone, will not be implemented here. Instead they must be inherited and overridden.

Open up the file sum_ga.py. This contains an example class that overrides these methods. As you implement methods in the GeneticAlgorithm class, you will call them in the main program of this file to ensure that they are working as expected. Build your implementation incrementally, testing each new set of methods as you go.

1. Start by implementing the methods initializePopulation and evaluatePopulation.

   To test them, modify the main program in the file sum_ga.py. Create an instance of the SumGA class where the length of the candidate solutions is 10 and the population size is 20. Use this instance to call the methods that you implemented. Next, add a for loop to print out each member of the population, and its fitness. Finally, print out the class variables you created to track the best ever fitness and best ever candidate solution. Ensure that they have been set correctly based on your initial population. To execute your test code do:

       python3 sum_ga.py
     

2. Now implement the three main operators used in a genetic algorithm: selection, crossover, and mutation. Below is a review of how each of these operators function.

   • The selection method takes no parameters and stochastically chooses a candidate solution from the current population based on its fitness. The probability of choosing a particular candidate solution is the ratio of its fitness to the total fitness of the entire population. Here is a pseudocode for achieving this:

     spin = random() * totalFitness
     partialFitness = 0
     loop over the popSize
        partialFitness += scores[i] 
        if partialFitness >= spin:
           break
     return a COPY of individual[i]
     

     Test that selection is working correctly. Use a loop to repeatedly select members of the population. Check that the most fit members are getting selected more often than the least fit members.
   • The crossover method takes two parents as input. The class variable self.probCross represents the probability that crossover will occur for any two parents. When crossover doesn't occur, simply return the two parents. When crossover does occur, a random crossover point between 1 and the length of the parent-1 should be determined. For example, if the parent was 16 long, then the crossover point should be randomly chosen to be between 1 and 15. The first child should be created by taking parent1's values starting from the beginning and continuing up to, but not including the crossover point. The remainder of the first child should be created by taking parent2's values starting from the crossover point and continuing to the end. The second child should be created using the opposite portions of the two parents. An example is shown below.

     
               0  1  2  3  4  5  6  7
     parent1: [1, 1, 1, 0, 0, 0, 0, 0]
     parent2: [0, 1, 0, 1, 0, 1, 0, 1]
                       ^ 
     crossPoint:       3
     
     child1:  [1, 1, 1, 1, 0, 1, 0, 1]
     child2:  [0, 1, 0, 0, 0, 0, 0, 0]
     

     Test that your crossover method is working properly by printing out the parents, the selected crossover point, and the resulting children.
   • The mutation method takes a child and uses the class variable self.probMutate. For each position in the child it uses the probability to determine whether that particular position should be modified. When making a mutation, you should flip the bit. If it's a 1 it becomes a 0, and if it's a 0 it becomes a 1. An example is shown below.

     child before mutation:  [1, 1, 1, 1, 0, 1, 0, 1]
     child after  mutation:  [1, 0, 1, 1, 0, 1, 1, 1]
     

     Because the child is represented as a list, any change you make will be permanent, so this method does not need to return anything.
     
     Test that your mutation method is working properly by printing out the incoming child and the child after mutation is completed. Remember that it is possible for none of the positions in the child to be mutated and it is also possible for multiple positions on the child to be mutated.

3. Implement the method oneGeneration that replaces the current population with a new population generated by applying the three operators: selection, crossover, and mutation. Pseudocode is shown below:

   initialize the newPopulation to an empty list
   loop until the size of newPopulation >= the desired popSize
      select parent1
      select parent2
      child1, child2 = crossover(parent1, parent2)
      mutate child1
      mutate child2
      add child1 and child2 to the newPopulation
   if size of newPopulation is > desired popSize
      randomly choose one child to remove
   population = newPopulation
   increment generation counter
   

   Test this method and see if the average fitness of the next population is higher than the average fitness of the previous population.

4. Implement the method evolve that repeatedly calls oneGeneration until the maximum number of generations has been reached or the isDone method returns True. Pseudocode is shown below:

   set class variables given in parameters
   initialize a random population
   evaluate the population
   while generation < maxGeneration and not done
      run one generation
      evaluate the population
   return the best ever individual
   

5. If your genetic algorithm is working properly, then the following main program for the file sum_ga.py should yield a graph similar to the one shown below.

    def main():
       # Chromosomes of length 20, population of size 50
       ga = SumGA(20, 50)
       # Evolve for 100 generations
       # High prob of crossover, low prob of mutation
       bestFound = ga.evolve(100, 0.6, 0.001)
       print(bestFound)
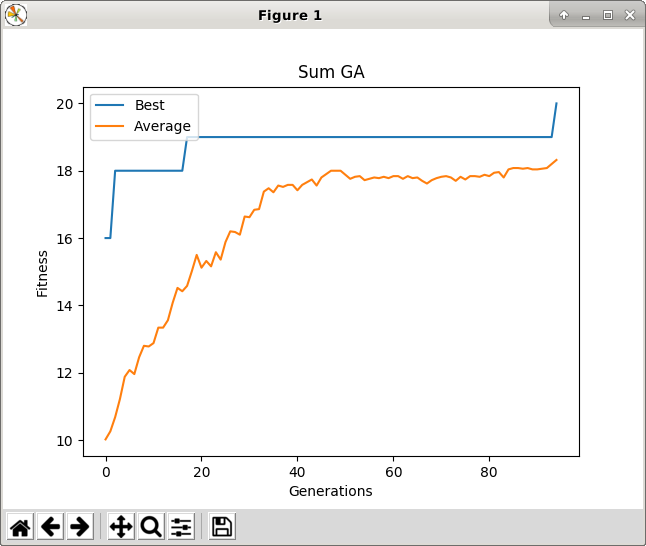
       ga.plotStats("Sum GA")
   



Once you are convinced that the genetic algorithm is working properly, you will then move on to creating a specialized genetic algorithm that can evolve the weights and biases of a neural network.

Implement the NeuralGA class

Open the file neural_ga.py. This class is a specialization of the basic GeneticAlgorithm class. Rather than creating chromosomes of bits, it creates chromosomes of neural network weights (floating point numbers). There are only two methods you need to re-implement: initalizePopulation and mutate.

There is some test code provided that creates a population of size 5 of a small neural network with an input layer of size 2, an output layer of size 1, and no hidden layers. To execute this test code do:

    python3 neural_ga.py
  

You should see that each chromosome contains small random weights and that about 50 percent of the weights get mutated to new small random weights.

Once this is working, you are ready apply your NeuralGA class to a reinforcement learnng problem.

Implement the RLNeuralGA class

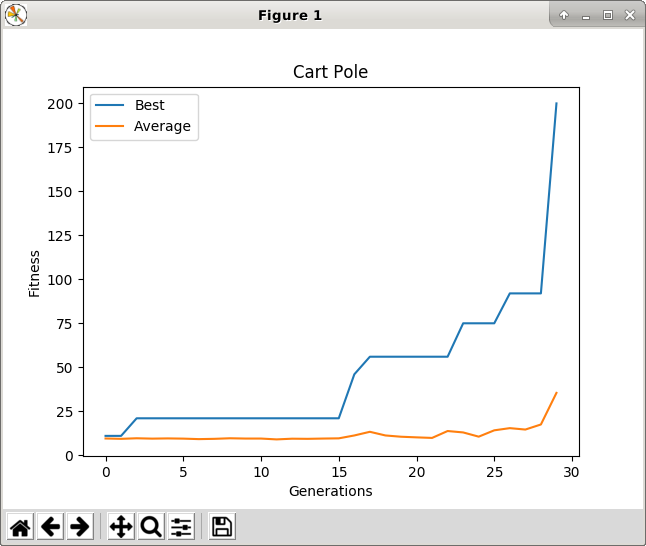
In Lab 7, we used approximate Q-learning to solve the Cart Pole problem. We accomplished this by approximating the Q-learning table with a neural network. The inputs to the neural network were the states of the problem and the outputs were the estimated Q-values of doing each action in the given state. We applied back-propagataion to learn the weights, using the Q-learning update rule to generate targets for training.

Now that you have implemented GAs, we can tackle reinforcement learning problems in a new way. We will again use a neural network to represent the solution. Like before, the inputs to the network will represent the states of the problem, but now the outputs will represent the actions directly. Our goal will be to find a set of weights for the network such that the total reward received when following its action outputs is maximized. We will accomplish this by generating a population of random weight settings, and go through generations of selection, crossover, and mutation to find better and better weights. The fitness function will be the total reward received over an episode of choosing actions using the neural network.

The benefits of this approach over Q-learing are that now our actions need not be discrete, and our policy for behavior is much more direct--we are not learning values first, and then building a policy from them. We will compare the GA to Q-learning at solving the Cart Pole problem.

Open the file rl_neural_ga.py and complete the methods fitness and isDone. Here is pseudocode for the fitness method:

  create a neural network with the appropriate layer sizes
  set the weights of the network using the chromosome
  state = reset the env
  initialize total_reward to 0
  loop over steps 
     check whether to render the env
     output = forward propagate the state through the network
     choose the action with the maximum output value 
     step the environment using that action
     observe the state, reward, and whether episode is done
     update total_reward using the current reward
     when done, break from the loop
  return total_reward

In order to use OpenAI Gym you'll need to activate the CS63 virtual environment:

source /usr/swat/bin/CS63-10.1

To run the code do:

python3 rl_neural_ga.py

You should find that the GA can fairly quickly discover a set of weights that solve the Cart Pole problem.



Submitting

Use git to add, commit, and push the files that you modified.