- For each data structure covered in the course, come up with a
real-world application that motivates the data structure. The data structure
should be able to provide a more efficient solution to the problem then any
other structure covered so far.
- Give a binary tree with integer keys at nodes, whose traversals are:
- PreOrder: [80 46 92 90 121 111 105]
- InOrder: [46 80 90 92 105 111 121]
- PostOrder: [46 90 105 111 121 92 80]
Is the tree a BST? Is it an AVLTree? Justify your response.
- Consider the following tree:
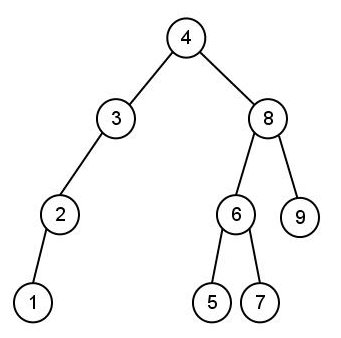
- What is the pre-order traversal of the tree?
- What is the in-order traversal of the tree?
- What is the post-order traversal of the tree?
- What is the level-order traversal of the tree?
- Identify if it is a tree, binary tree, BST, AVL tree
- Based on your previous answer, draw the tree obtained by inserting
10 into the tree.
- Draw the tree obtained by deleting 2 from the tree.
- Draw both trees that might be obtained by deleting 4 from the tree while
still maintaining the properties in your answer to e)
- Consider a boolean function LinkedBST::containsInRange that
takes as arguments two keys -- min and max --
and returns true if there exists a key k in the tree
such that min <= k <= max. One possible implementation of
this function is to call a recursive helper function that takes
an additional argument -- a node in the tree, and returns whether that
subtree contains any keys in the range:
template <typename K, typename V>
bool LinkedBST<K,V>::containsInRange(K min, K max) {
return subtreeContainsInRange(root, min, max);
}
Write the recursive helper function subtreeContainsInRange.
You may assume that empty trees are represented by pointer to a NULL
node.
- For each of the code fragments below, draw the AVLTree that
results from the code fragment:
-
AVLTree<int,int> t;
for (int i = 1; i <= 10; ++i) {
t.insert(i,i);
}
-
AVLTree<int,int> t;
for (int i = 1; i <= 5; ++i) {
t.insert(i,i);
t.insert(-1*i,-1*i);
}
-
AVLTree<int,int> t;
for (int i = 1; i <= 5; ++i) {
t.insert(i,i);
t.insert(11-i,11-i);
}
- For each of the three code fragments above, draw the tree that would
result if a LinkedBST were used instead of an AVLTree.
- What is the worst-case running time of the following function? Use
Big-O notation.
void f(int n) {
if (n < 0) {
return;
}
AVLTree<int,int> t;
for (int i = 0; i < n; ++i) {
t.insert(i,i);
}
for (int i = 0; i < n; ++i) {
cout << t.remove(i) << endl;
}
}
- What is the smallest AVL tree such that removing a node requires a
rotation to rebalance the tree? (There is more than one correct answer, but
they're all the same size.)
- What is the smallest AVL tree such that removing a node requires
two rotations to rebalance the tree? (Again there is more than one correct
answer, but they're all the same size.)
- For each of the code fragments below, draw the BinaryHeap that
results from the code fragment, and draw its final array-based representation:
-
BinaryHeap<int,int> heap;
for (int i = 1; i <= 10; ++i) {
heap.insert(i,i);
}
for (int i = 1; i <= 5; ++i) {
heap.removeMax();
}
-
BinaryHeap<int,int> heap;
for (int i = 10; i > 0; --i) {
heap.insert(i,i);
}
-
BinaryHeap<int,int> heap;
for (int i = 1; i <= 5; ++i) {
heap.insert(i,i);
heap.insert(-1*i,-1*i);
}
- What is the worst-case running time of the following function? Use
Big-O notation.
void f(int n) {
if (n < 0) {
return;
}
BinaryHeap<int,int> heap;
for (int i = 0; i < n; ++i) {
heap.insert(i,i);
}
for (int i = 0; i < n; ++i) {
cout << heap.removeMax() << endl;
}
}
