In addition to all concepts from Quiz 1,

You should be able to define or explain the following terms:

• Abstract data types; interface vs. implementation; advantages to using ADTs
• The List interface, including implementation details and runtime analysis using array lists, linked lists
• Divide and conquer
• Recursion trees
• Merge sort and merge
• Quick sort, partition, randomized quick sort, and pivot
• Concepts related to sorting: runtime, comparisons, swaps.
• Stack interface and operations
• Queue interface and operations
• Depth-first and breadth-first search
• Dynamic memory management and responsibilities
• Induction
• Invariant

You should be familiar with the following C++-related concepts:

• Segmentation fault.
• new and delete for basic types, one-dimensional arrays, and two-dimensional arrays
• Roll of class destructors and constructors
• Pointer/array equivalence
• Abstract (or pure virtual) classes
• Templates
• this pointer
• comparison operators

Practice problems

1. You should be able to implement all of the methods of LinkedList and ArrayList classes as well as provide a stack trace of a sample main() program. Declare and implement a new method for ArrayList , replaceItem(int i, T val), that replaces the existing value at position i with val. It should return the previously held value.


2. Define replaceItem for a templated LinkedList implementation. Compare and contrast the expected run time with the ArrayList implementation.


3. Write a program that prompts the user for an integer n, then reads n strings into an array of strings stored on the heap, prints true if the array is sorted and false otherwise, and then frees the memory on the heap. As part of this program declare and implement a templated boolean isSorted(T* a, int n) function that, given a pointer to an array a and the length of that array n, returns true if the array is sorted and false otherwise.


4. In class, we defined a Queue using various List implementations. Let's flip this around. Consider the following (somewhat strange) List definition, QueueList, that uses an awesomely cool MagicQueue to represent the data in the list. (Note that the details of MagicQueue are not given, but are also unnecessary given what you know about interfaces.)

    
       #pragma once
    
       #include "list.h"
       #include "magicqueue.h"
    
       template <typename T>
       class QueueList : public List<T> {
         private:
           MagicQueue <T> values;
   
         public:
           QueueList();
           ~QueueList();        
           void insertAtHead(T item);
           void insertAtTail(T item);
           int getSize();
           bool isEmpty();
           // ...etc. all List methods are declared here
       };
    
       #include "queuelist-inl.h"
    

   Using the above declarations, complete an implementation for the methods getSize(), insertAtHead(T item), and removeTail(). Your answers should be written as they would appear in queueList-inl.h, paying attention to the scope and template operators. Once complete, describe the O() of each of your methods. Again, the details of MagicQueue are not important; you should assume it implements a Queue interface properly in O(1) time.

   
   
5. Consider the following somewhat simplified map of Sharples:
   
   
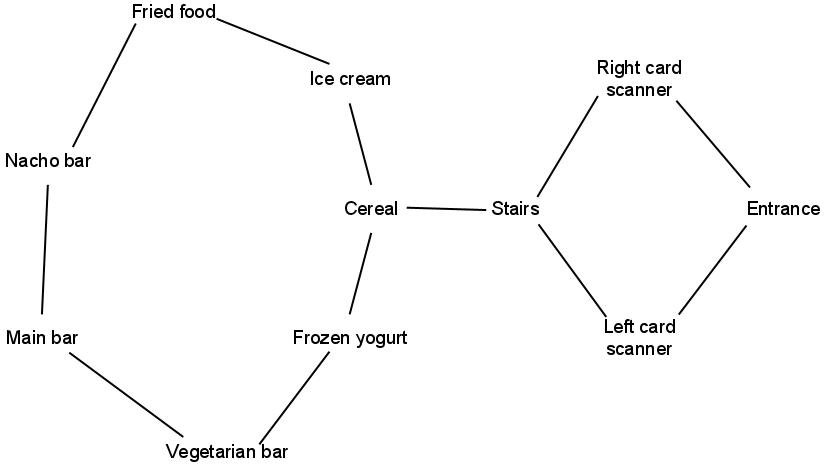
   • Use depth-first search to find a path from the Entrance to the Fried food location. Carefully track the data used by depth-first search as the algorithm runs.
   • Use breadth-first search to find a path from the Entrance to the Fried food location. Carefully track the data used by breadth-first search as the algorithm runs.
   
   
6. Trace and show work for sorting a set of integers using both merge sort and quick sort. In particular, be able to see how the helper methods merge and partition are used.
7. Consider the following algorithm, wackyMergeSort, similar to mergeSort:

    
       wackyMergeSort(A, n):
         if (n <= 1)
           return
         A1 = new array
         A2 = new array
         copy first two-thirds (2n/3)  of A into A1
         copy last  one-third (n-2n/3) of A into A2
         wackyMergeSort(A1, 2n/3)
         wackyMergeSort(A2, n-2n/3)
         // merges sorted A1, A2 back into A
         merge(A1, 2n/3, A2, n-2n/3, A) 
   

   • Is wackyMergeSort a correct sorting algorithm?
   • Draw a recursion tree for wackyMergeSort on an input of size n. For each node (recursive call) in the recursion tree, write the amount of work you expect to be done for just that recursive call to wackyMergeSort. Use Big-O notation for all parts of this problem, justifying (but not proving) your work.
   • How much total work is done per level in the recursion tree?
   • How many total levels are in the tree?
   • Overall, how much total work is done for wackyMergeSort for an input of size n?
   
   
8. Loop Invariants. For each of the following algorithms, prove the algorithm is correct by using a loop invariant. First, explicitly state the loop invariant. Then, show how the loop invariant implies the algorithm works. Finally, prove the loop invariant using induction.
   1. adding all elements of a list

      Algorithm sum(A, n):
        Input: An array of n numbers
        Output: The sum of all elements in the array
      
        toReturn = 0
        for i=0...n-1
          toReturn = toReturn + A[i]
        return toReturn
            

   2. checking to see if an array is sorted

      Algorithm isSorted(A, n)
        Input: An array A of n elements
        Output: true if A is sorted, false otherwise
      
        for i =0...n-2:
          if(A[i] > A[i+1]):
            return false
        return true
            

   3. searching for an element in a sorted array.

      Algorithm binarySearch(A,n, x):
        Input: A sorted array of size n, an element of x we wish to find
        Output: Position of x, or -1 if not found
      
        low=0, high=n-1
        while(low < high):
          mid = (low+high)/2
          if(A[mid] == x) :
            return mid
          else if (A[mid] < x):
            low = mid+1
          else:
            high = mid-1
        return -1;
            

Home Page