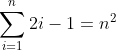You should be able to define or explain the following terms:

• data structure
• algorithm
• major differences between C++ and Python
• scope of a variable
• pass by value (a.k.a. copy by value), pass by pointer (e.g., arrays)
• object oriented programming and its major properties (e.g., abstraction, modularity, reusability, encapsulation)
• class
• instance of a class (i.e., object)
• function call stack
• the heap
• inheritance, is-a relationship
• base class, derived class (a.k.a., parent class, child class)
• polymorphism
• algorithmic analysis (e.g., how to count steps, how to evaluate loops)
• pseudocode (both interpreting and writing)
• asymptotic analysis and Big-O notation
• empirical analysis
• constant, logarithmic, linear, quasilinear (n lg n), quadratic, and exponential functions
• induction
• correctness of an algorithm
• loop invariants (I won't ask you to solve a loop invariant problem, but you should understand the general use and purpose)

You should be familiar with all aspects of basic C++ programs, such as those you created for labs 01 and 02. This includes:

• how to compile and execute C++ programs
• the int, float, char, bool, string data types
• variables, assignment with =, and basic arithmetic
• boolean and relational operators in C++
• if / else if / else statements, while loops, do-while loops, and for loops
• uses of break and continue
• variables, including their declaration, definition, and use
• functions, including their declaration, definition, and use
• arrays (statically allocated)
• basic uses of cout and cin
• basic uses of file streams (i.e., ifstream ofstream)
• purpose of #include and using namespace std;
• void and its use
• pointers, referencing, dereferencing, NULL
• dynamic memory management with new and delete (not for arrays)
• classes, including their declaration and implementation as well as the use of access control: public, private, and protected, data members, functions, constructors, destructors
• C++ inheritance, calling parent constructor/methods, virtual, pure virtual
• dot notation and arrow notation
• tracing a program using a memory diagram (heap and stack)

Practice problems

1. Write a C++ program that prompts the user for an integer n and then prints a single output integer, the sum of the integers from 1 to n.


2. Write a boolean function isPrimaryColor that takes a string as an argument and returns true if the string is "red", "yellow", or "blue", and returns false otherwise. Then write a program that prompts the user for a color and uses isPrimaryColor to determine if their color is primary.


3. Draw a memory diagram for cs35/class/02/inheritance/testPerson.cpp as it executes. Include the stack and the heap.


4. Write a Shape class with the following features:
   • private color (a string) data member.
   • a constructor which takes in a color and initializes the color of the Shape.
   • appropriate public getColor(), setColor() and print() accessor functions. print() should output the color of the object, e.g. "Shape with color black."
   Then write a Rectangle subclass of Shape with the following features:
   • a private length and width (both int) data members
   • a constructor which takes a color, length, and width, which it uses to initialize the data members.
   • accessor functions: getArea() and print(). print should output the area and color of the Rectangle, e.g. "Rectangle with area 20. Shape with color black."
   Finally, write a main() function that declares a pointer p to a Shape, creates a single Rectangle on the heap and saves the pointer to that Shape as p, and then prints the Shape and releases its memory.


5. In cs35/class/02/account you will find an implementation of a BankAccount class and a test file. Trace through the main program. Then, add and implement an ability to deposit money into the account and test it out in the main program


6. Prove that 41*n^2 + 12n - 1 is O(n^2).


7. Using induction, prove that 0^2 + 1^2 + 2^2 + ... + n^2 is less than or equal to n^3 for all non-negative integers n. NOTE: for this problem, it is easier to assume the proposition is true for n and then prove that is also true n+1


8. Prove by the following by induction for all values n ≥ 1:
   

Home Page