The goal of this lab is to learn about recursion. You will write three programs that make calls to recursive functions. Some of these are based on producing fractal patterns and will use the graphics library.

To start, run update21 to create the cs21/labs/11 directory.

Towers of Hanoi is a puzzle consisting of three pegs and some number of disks, each with a different diameter. At the start of the game, the disks are arranged on peg 1 as a tower (the largest disk on the bottom, followed by the second largest, ..., followed by the smallest on top). The goal is to move the tower to the third peg. At each step only a single disk can be moved from one peg to another, and at no point can a larger disk cover a smaller disk. The wikipedia page for towers of hanoi explains more about the puzzle.

In a file named towersofhanoi.py you will implement two versions of a function that count the number of minimum number of steps needed to solve the Towers of Hanoi problem. Both functions solve the same problem, but one uses an iterative algorithm while the other uses recursion. Both functions take as a parameter the number of disks to move and both return the minimum number of steps it takes to solve a Towers of Hanoi puzzle for the given number of disks. NOTE: you are not solving the actual problem, but rather counting the steps needed to solve the problem. Section 13.4.1 of the book has a description of the actual Towers of Hanoi problem.

Your main program should:

• Get the number of disks in the tower from the user.
• Call your iterative function to get the number of steps.
• Print the results of your iterative function.
• Call your recursive function to get the number of steps to solve the Towers of Hanoi problem.
• Print the results of your recursive function.

The number of steps to solve a puzzle with N disks is defined by the following recursive definition:

1. a 1 disk puzzle takes 1 step (move the disk from peg 1 to peg 3)
2. a puzzle of N disks takes 1 plus 2 times the number of steps it takes to solve the puzzle with N-1 disks

Thus,

 for 1 disk it takes 1 step
 for 2 disks it takes 1 + 2 times the number of steps to solve for 1 disk =  3 
 for 3 disks it takes 1 + 2 times the number of steps to solve for 2 disks = 7 
 for 4 disks it takes 1 + 2 times the number of steps to solve for 3 disks = 15 
 ...

Here are some sample runs of a working program:

$ python towersofhanoi.py
This program computes the minimum number of steps it takes
to solve a Towers of Hanoi puzzle of a given number of disks.
Enter the number of disks in the puzzle: 3
For a Towers of Hanoi puzzle of size 3 it takes:
        7 steps (iteratively)
        7 steps (recursively)

$ python towersofhanoi.py
This program computes the minimum number of steps it takes
to solve a Towers of Hanoi puzzle of a given number of disks.
Enter the number of disks in the puzzle: 5
For a Towers of Hanoi puzzle of size 5 it takes:
        31 steps (iteratively)
        31 steps (recursively)

$ python towersofhanoi.py
This program computes the minimum number of steps it takes
to solve a Towers of Hanoi puzzle of a given number of disks.
Enter the number of disks in the puzzle: 10
For a Towers of Hanoi puzzle of size 10 it takes:
        1023 steps (iteratively)
        1023 steps (recursively)

Recursion can be used in graphics to produce realistic natural images, such as ferns, trees, and terrain. For this program, you will use the midpoint displacement algorithm to create a realistic one-dimensional terrain map (think of a mountain ridge line).

The midpoint displacement algorithm, using recursion, is as follows:

• start with two points A and B
• if the recursive level is 0, just draw the line from point A to point B
• if the recursive level is greater than 0, find the midpoint C (i.e., the point half-way between A and B). Displace C vertically a small random amount, then recur twice, once using points A-C and the other using points C-B
• each time the function recurs, the level should decrease by one

Here are four examples of 1D terrains for recursive depths 0 (the straight line) to 3:

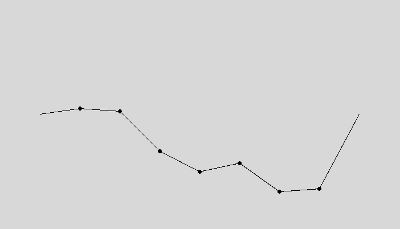
Note: in the above sample images, I drew the midpoints to help you understand the problem. Your program does not need to draw dots at each midpoint.

Requirements and Details:

In a file named terrain.py, write a program to create a one-dimensional terrain map, using a recursion depth given by the user. Your program should:

• ask the user for the recursion depth
• open a graphics window that is wider than tall (700x400 works well)
• call a recursive function to create and draw the terrain (use the midpoint displacement algorithm above)
• wait for a mouse click before closing the window

Hints and Tips

• Remember that to use the graphics and random libraries, your program needs to import them:

   
    from graphics import *
    from random import *
    

• You will need to define values for A and B when making your initial call to the recursive function. For a window of height height and width width, define the x and y values of A and B as follows:

    xA = 0.1*width
    xB = 0.9*width
    yA = height/2
    yB = height/2
    

• When making your two recursive calls, you will need to calculate the midpoint C that lies half-way between A and B. The y-value of C should be adjusted some random amount to create a realistic look. You can use the following formula to calculate the range of adjustment values:

    changeX = distance between xA and xB  
    rangeY = changeX/4+1
    

  You should then sample a displacement value randomly between -rangeY and rangeY and add it to the midpoint value. There are other methods for calculating random displacement, so feel free to try something else. Your displacement factor, however, should get smaller as you get into deeper levels of recursion.
• Debuging: you can add in calls to sleep(0.05) to slow down the recursion and see what it gets drawn at each step. Adding debug print statements to print out the point (x,y) coordinates at each recursive call may also help. Just remember to remove both debug print statement and debug calls to sleep before your submit your solution.

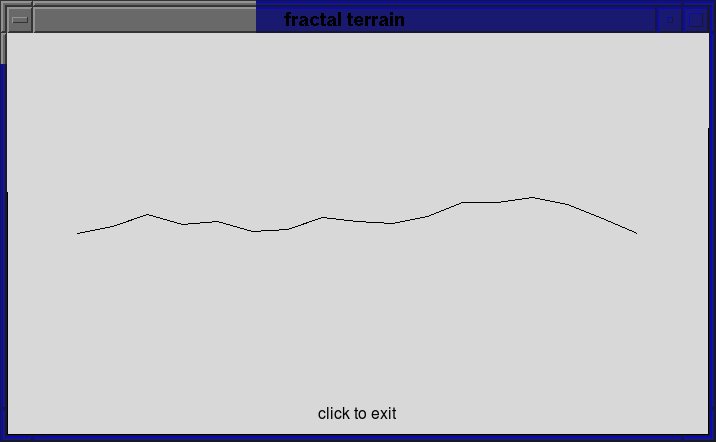
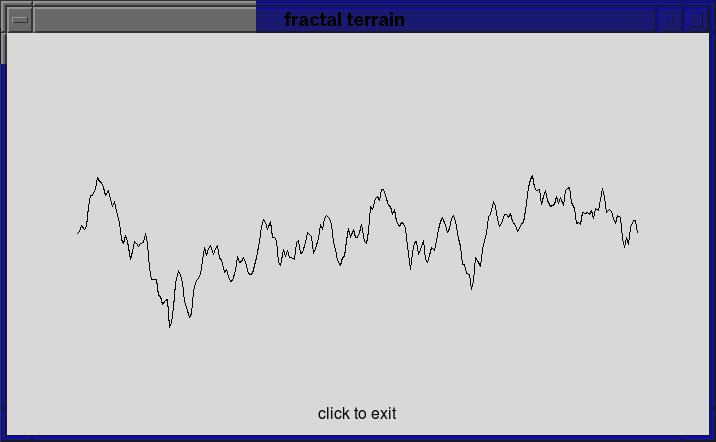
Here is the output from two runs of a working program, the first one the user enters 4 for the level value, the second one the user enters 8 (yours will not be identical to these due to the random change in y value at each step, but the amount of detail should be similar):

You will implement a program, fractalsquares.py that recursively draws a pattern of squares to the graphics window. Your program will:

1. create a square graphics window (e.g., 500 by 500) and set the background to black.
2. prompt the user to enter a depth value.
3. call your recursive drawsquares function to recursively draw a fractal pattern of squares for the given depth of recursion.
4. wait for the user to click in the graphics window to exit.

For example, here are the results of two runs of a working program, the first is for a level 1 pattern, the second for a level 3 pattern:

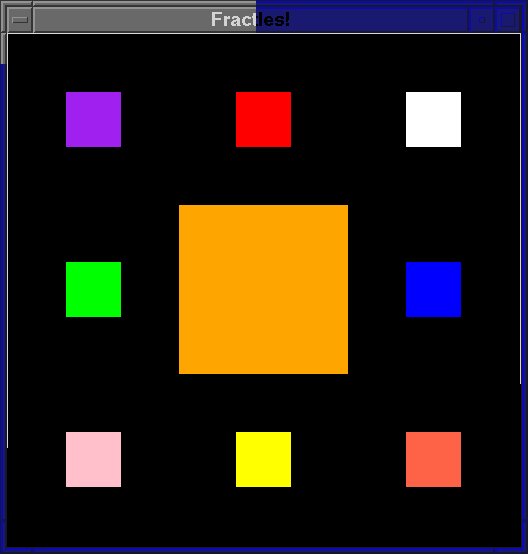
This pattern is based on recursively spliting the window into 9 even sub-squares. The center square will be filled with the passed in color. The other 8 should be recursively filled with squares of dimension one third of the current square's size.

Your recursive squares function should do the following:

• Divide the current square into 9 smaller squares.
• If the depth level is 0: simply fill in the center square centered at the given point in the graphics window, using the passed in color.
• otherwise, you will make recursive calls. First, fill the center square with the passed in color. The other eight squares will be filled by making recursive calls to draw smaller squares (at the next smallest depth level) based on the sub-square's location and width.
• Each of the eight recursive calls should draw a square of a different color. Use colorPicker to find colors in the graphics library.

For this problem, we are leaving it up to you to figure out what you need to pass to your recursive function at each step. Think about what the function needs to determine if it needs to make further recursive calls or stop the recursion, and what it needs to know to draw a square to the graphics window at the appropriate position of the appropriate size of the appropriate color.

HINT #1: you should worry about picking colors after you figure out your recursion. You can start off by drawing all squares the same color, like blue.

HINT #2: work on the base case first. Next, figure out how to match the examples at level 1 and level 3. You can first try recurisively drawing just one of the eight smaller square's contents, for example the one to the right. Once you have that working, then add in code to recursively draw each of the eight sub-squares.

As always, this is not required and should only be attempted once the regular three parts are working correctly. The first suggested challenge problem is mostly for fun, the second problem, however, is more difficult than the required three, and thus more of a challenge, and the third even more challanging still.

1. Cooler than Squares

You could add an extension to the fractal squares problem to draw a more complicated shape than a square each time. For example, if you draw the square and then draw four smaller black squares in each corner, you could draw a plus sign at each step. If you want to try out a more interesting shape, cp your fractlsquares.py file to fractalextra.py and add the more interesting shape in this file:

$ cp fractalsquares.py fractalextra.py
$ vim fractalextra.py

You could also play around with the colors too.

2. Koch curves

Below are examples of six Koch curves that have recursion depths from 0 (a straight line) at the top to 5 at the bottom.

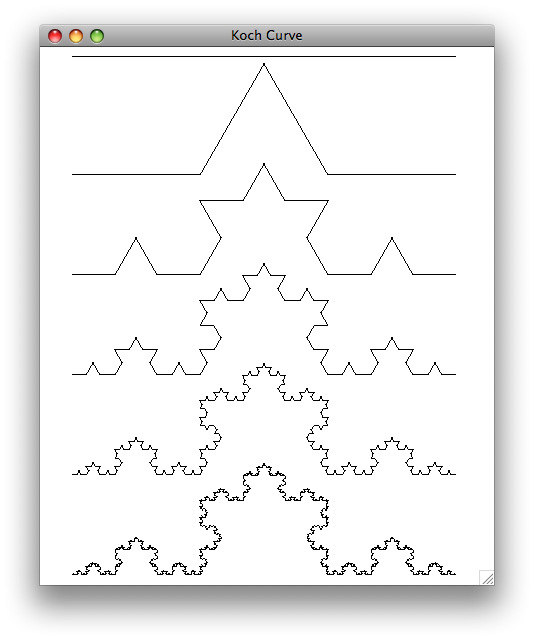
A Koch curve is created by breaking a line segment into thirds and replacing the middle segment by two segments that are equal in length. This creates a two-sided equilateral triangle in the middle (e.g., all angles are 60 degrees).

You should start by creating a program called koch.py. You will write a function:

drawKochCurve(win, n, start, end, angle)

which draws a Koch curve from point start to a point end with recursion depth n where angle specifies the angle of the line that connects start to end.

A Koch curve of recursion depth n is formed by four Koch curves as follows:

1. drawing a Koch curve of length length/3 with degree n-1 and angle
2. drawing a Koch curve of length length/3 with degree n-1 and angle-radians(60)
3. drawing a Koch curve of length length/3 with degree n-1 and angle+radians(60)
4. drawing a Koch curve of length length/3 with degree n-1 and angle

Hint: Each one of these recursive calls is starting from a different starting point.

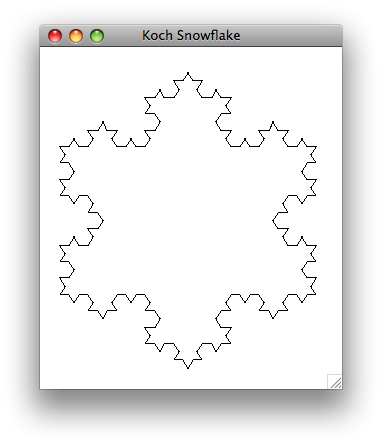
3. Koch snowflake

Once you have successfully created a single Koch curve, you can try puting three Koch curves together to create a Koch snowflake (cp your koch.py to kochsnowflake.py). The snowflake shown below is an example of a Koch snowflake made with 3 Koch curves.

Once you are satisfied with your programs you can hand them in by typing handin21 in a terminal window. Remember, there are three seperate files to hand-in this week.