CS21 Lab 11: Recursion
For this lab you will write several relatively small programs. This lab is a bit more like some of the earlier labs, except all of the programs will involve recursive function calls. In contrast to recent labs, there is less emphasis on modularity and large-scale program structure. However, that does not mean you should abandon good programming practices like making function-level comments and testing incrementally.
First, run update21, if you haven't already, to create the cs21/labs/11 directory. Then cd into your cs21/labs/11 and work on the starter files you find there. You should not need to create any new files.
You should write your solution to this exercise in palindrome.py. Palindromes are phrases where the list of letters is the same whether you read the text normally (from left to right) or in exactly the reverse order. Here are some examples: www.palindromelist.net
For this exercise you are going to write a function that recorgnizes "palindromic" lists. The function should take a list as a parameter and return True if the list is palindromic and False otherwise. Here are some example lists and the value your function should return.
| Input list | Return value |
| [1, 2, 3, 2, 1] | True |
| [1, 2, 3, 2, 4] | False |
| ["hello", 2.5, 2.5, "hello"] | True |
| [] | True |
| [1, 1.2] | False |
One small wrinkle that we're throwing in is that you should ignore None objects. This is similar to how spaces and punctuation are treated in normal palindromes. Here are some examples that include None:
| [1, None, 2, 3, 2, 1, None] | True |
| ["hello", 2.5, 2.5, None, "hello"] | True |
| [None, None, None, 3] | True |
In other words, a list with None objects is palindromic if the list you would get by filtering out the Nones is palindromic. Note: None is a special Python value that is usually used to indicate there is no real data. For example if you wrote a function to find the minimum number in a list of numbers, it would be reasonable to return None for the empty list. None is used in the Zelle graphics library as a return value from checkMouse, when there is no mouse click to report.
The interesting part of this exercise is the constraints on how you implement your palindromic function. You may not use:
- Loops (for, while, ...)
- Any built-in list functions/methods, except those explicitly listed below
- Any wacky list slicing expressions, except those explicitly listed below
You may use:
- Recursive function calls
- The len function
- The append method
- Simple indexing (e.g. items[42])
- Any slice that takes off the first, last, or both first and last elements (items[1:], items[:-1], items[1:-1]).
For the record, this is probably not how you would implement this function "in the real world". It's just a simple exercise to get you into writing recursive functions.
You should write your solution to this exercise in directories.py. For this exercise you will write a Python program that looks through a directory and all its sub-directories (and all their sub-directories, ...) and prints the names of files that match a given pattern.
The recursion in this exercise is over the directory heirarchy. Each recursive call should add an extra element to the file path. (For example, one call might go from a file path of "cs21/labs" to "cs21/labs/09".) The base case happens when the function hits a path that is a file (as opposed to a directory).
Note: the pattern applies only to file names, not directory names. If the pattern is '21', 'cs21/labs/10/filter.py' would not be considered a match. You can use the library function basename (described below) to get just the last part of a file path.
The starter code imports the following library functions, which your solution should use:
- listdir takes a string parameter, which should be a directory path. It returns a list of file and directory names that occur within that directory. For example, here is something you could see from listdir: listdir('cs21/labs') == ['05','01','06','02','04','08','09','10','11','00','07','03']
- isdir takes a string parameter, which should be a file/directory path. It returns True if the path is a directory and False otherwise. For example, isdir('cs21/labs') == True or isdir('cs21/labs/08/election.py') == False
- isfile is the complement to isdir. It returns True if the path is a file, and False otherwise. For example, isfile('cs21/labs') == False or isfile('cs21/labs/08/election.py') == True
- join takes two string parameters and combines them to make a complete path. For example, join('cs21/labs', '08') == 'cs21/labs/08'. This should seem like a very simple bit of string processing. The reason why there's a library function for it is that the conventions for directory path names are different on different systems; using this function makes your programs portable across systems.
- basename takes a file path parameter returns the part after the last directory separator. For example, basename('cs21/labs/08') == '08' or basename('cs21/labs/08/election.py') == 'election.py'.
For this exercise, you may use a loop to iterate over the list returned by listdir, but there should be no other loops in your solution.
The user interface for this program is a little different from others we have written. At the Linux prompt you can type:
$ python directories.py directory_name file_pattern
Also, you can make directories.py executable on Linux systems with the following command:
$ chmod +x directories.py
After the file is executable, you can just type:
$ ./directories.py directory_name file_pattern
Here is an example invocation of the program:
$ ./directories.py /usr/local/doc ro /usr/local/doc/intro.pdf /usr/local/doc/errors.html /usr/local/doc/prog-prove.pdf /usr/local/doc/StroudsCreek.pgm /usr/local/doc/intro-4.html /usr/local/doc/romeoandjuliet.txt /usr/local/doc/intro.html /usr/local/doc/text/romeo.txt /usr/local/doc/text/frost.txt /usr/local/doc/EnoToStroudsCreek.pgm /usr/local/doc/intro-3.html /usr/local/doc/intro-1.html /usr/local/doc/CULAProgrammersGuide.pdf /usr/local/doc/intro-2.html
You should write your solution to this exercise in yertle.py. For this exercise you will write a Python program that uses the Python turtle drawing library and recursive functions to draw some fun pictures. Turtle graphics was invented in the 1960s in the LOGO programming language as a simple and fun way to make line drawings. If you're not familiar, check out this video:
https://www.youtube.com/watch?v=oo7A1fPmPiE
The starter code for this exercise takes care of initializing the turtle library for you. For reference, here are the methods of the turtle object you will probably want to use:
- forward(dist) moves the turtle forward by dist units.
- right(degrees) rotates the turtle right (clockwise) by degrees° (which can be negative).
- left(degrees) rotates the turtle left (counter-clockwise) by degrees°.
- up() makes it so the turtle will not draw a line when it moves.
- down() makes it so the turtle will draw a line when it moves.
- heading() returns the direction the turtle is pointing in.
- position() returns the current position of the turtle. Example use: (pos_x, pos_y) = yertle.position().
- setPosition(x,y) moves the turtle to screen position (x,y).
- setHeading(h) rotates the turtle to heading h.
Drawing 1: Recursive Trees.
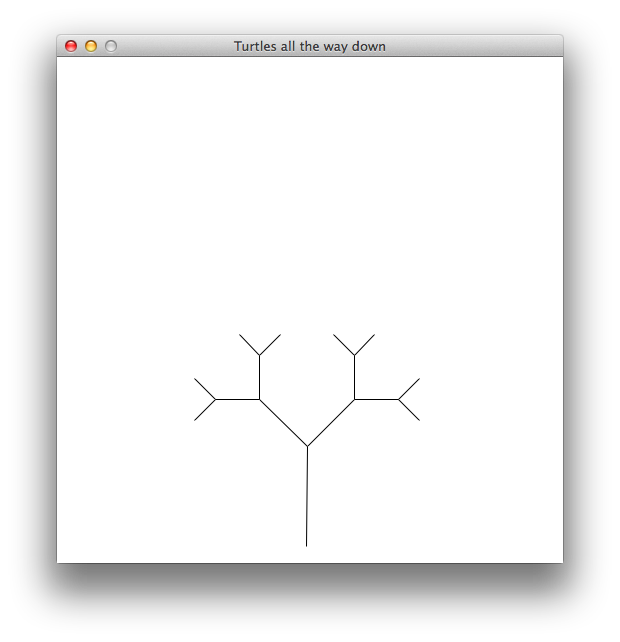
The first drawing is a branching tree. In this one, the turtle draws a stem of a given length, then draws two sub-trees 45° to the left and right from the end of the stem. Each subsequent stem should be shorter than its "parent" by the bushiness factor. Here you see some trees with different maximum stem lengths, minimum stem lengths and bushiness factors.
Max length: 200 — Min length: 5 — Bushiness: 2
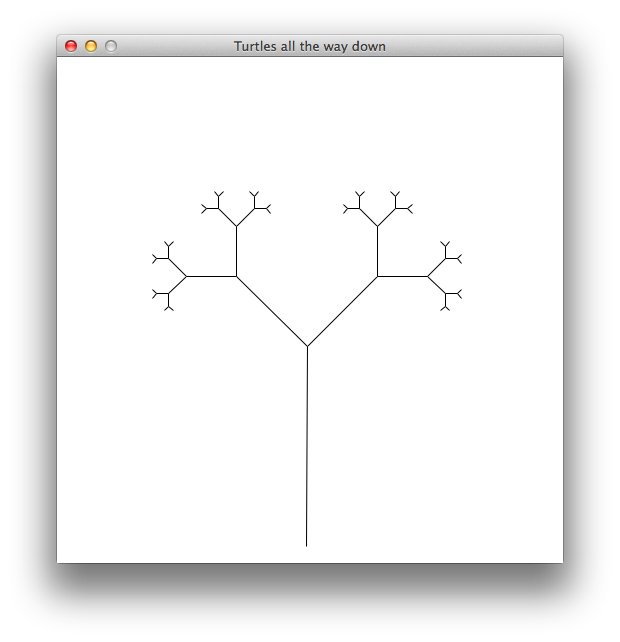
Max length: 150 — Min length: 5 — Bushiness: 1.5
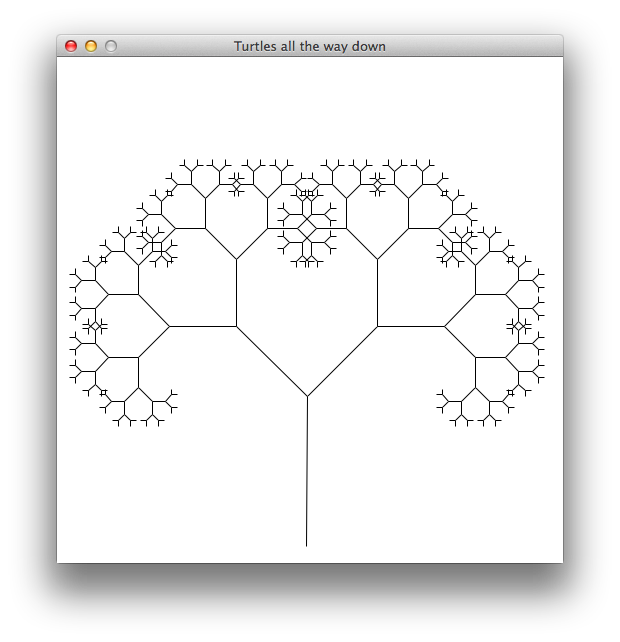
Max length: 150 — Min length: 10 — Bushiness: 1.5
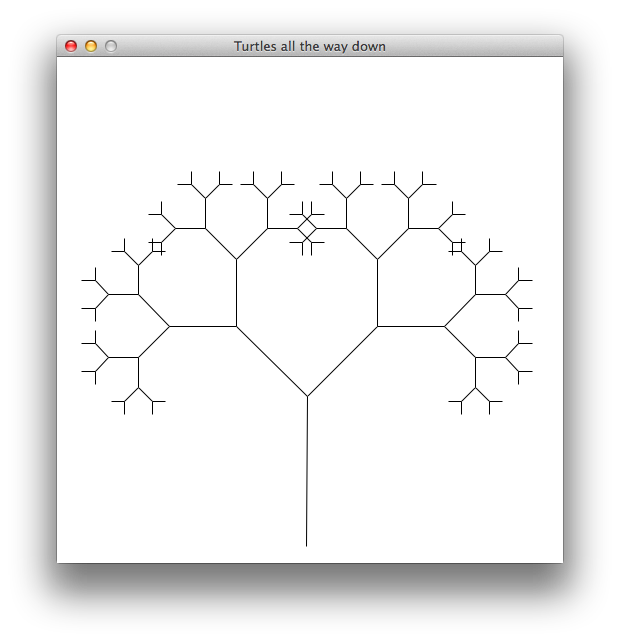
Max length: 100 — Min length: 20 — Bushiness: 1.5
The tricky part of this drawing is that after the turtle draws a sub-tree it needs to return back to where it was before it started on that part. You should accomplish this with the pos/heading and setpos/setheading methods.
Drawing 2: Sierpinski Triangles. A Sierpinski triangle is an image that has triangles nested within triangles. Here is an example:
You are going to write a turtle graphics function that approximates a Sierpinski triangle as the recursion depth is increased. Here are images generated from a solution for different values of line length and nesting depth. The first few don't look much like triangles, but the shape comes through more clearly in the later ones.
Line length: 200 — Depth: 0
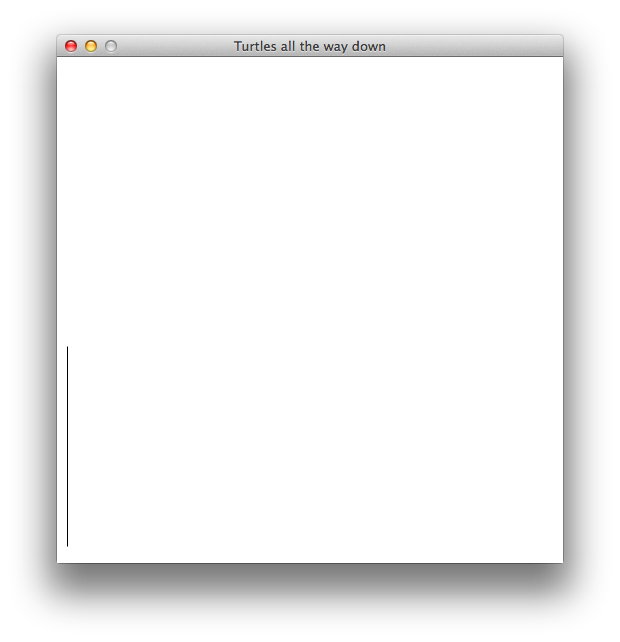
Line length: 150 — Depth: 1
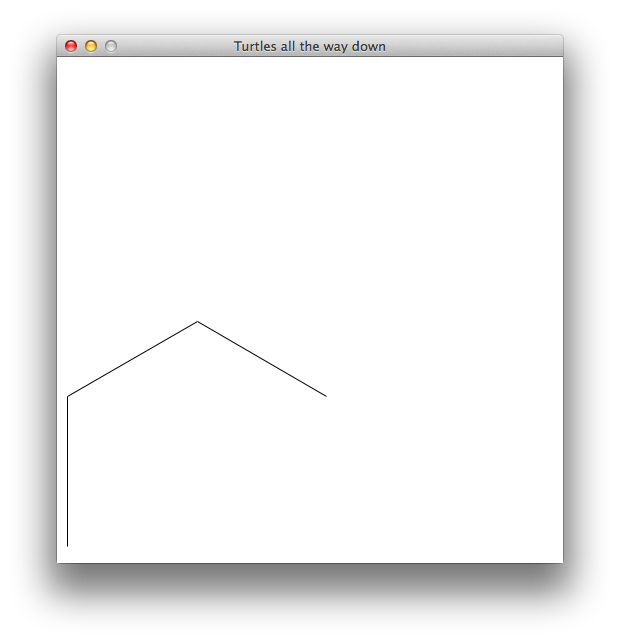
Line length: 100 — Depth: 2
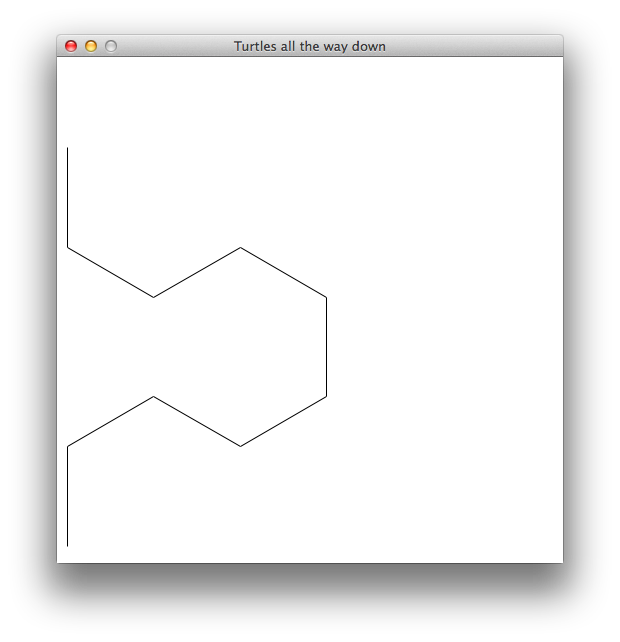
Line length: 60 — Depth: 3
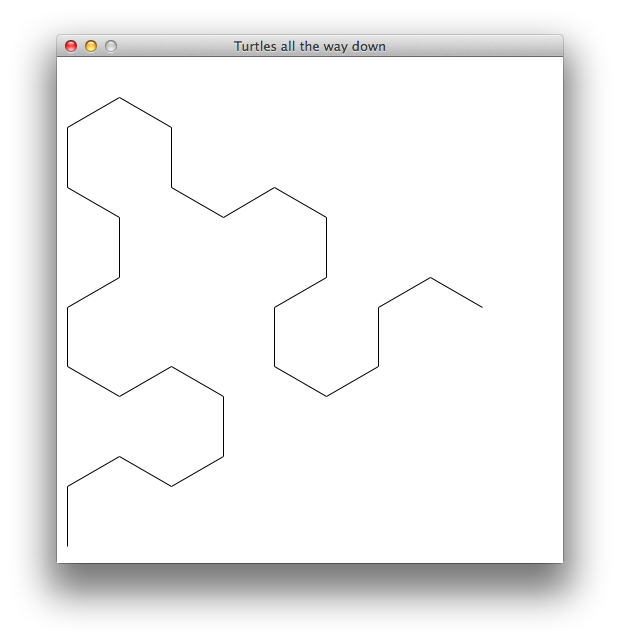
Line length: 30 — Depth: 4
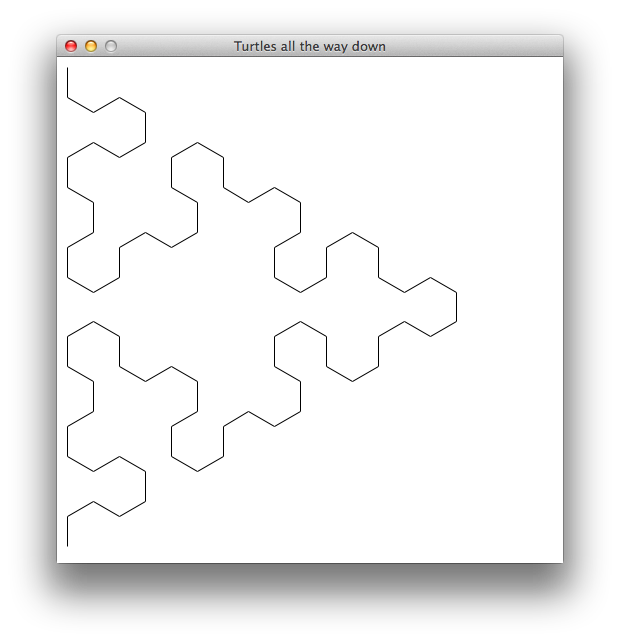
Line length: 15 — Depth: 5
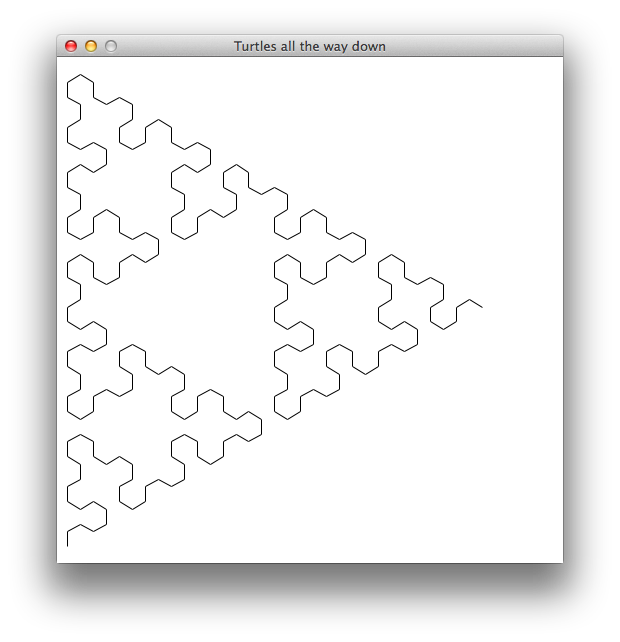
Line length: 8 — Depth: 6
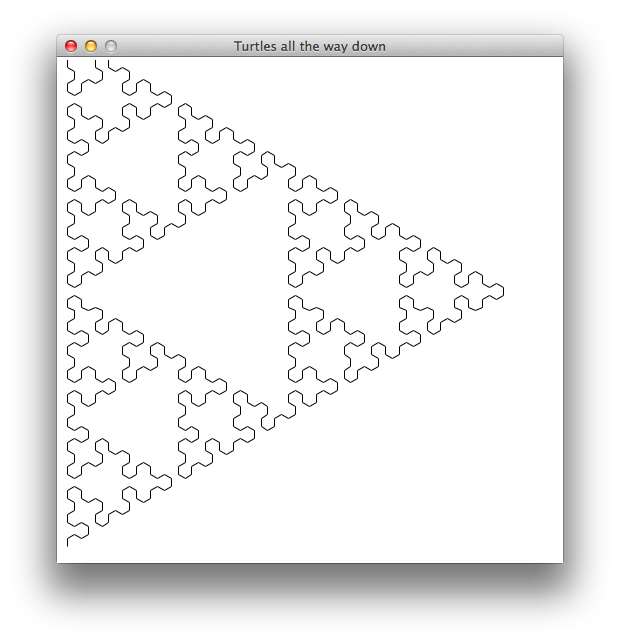
Line length: 3.5 — Depth: 7
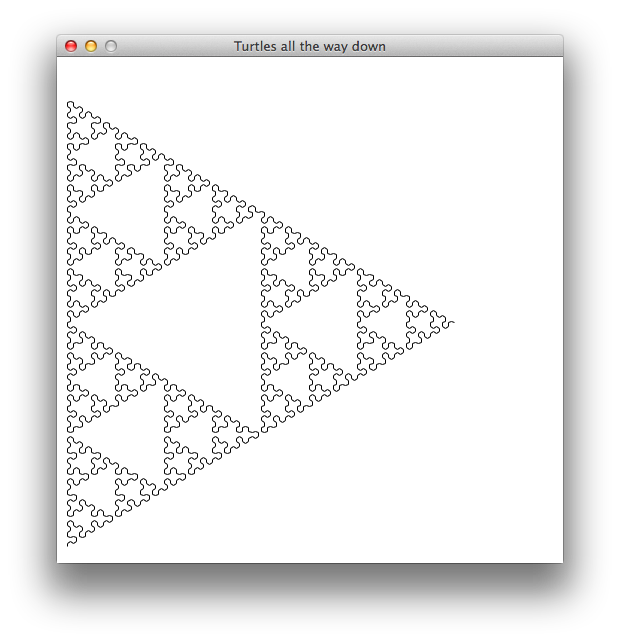
Line length: 1.8 — Depth: 8
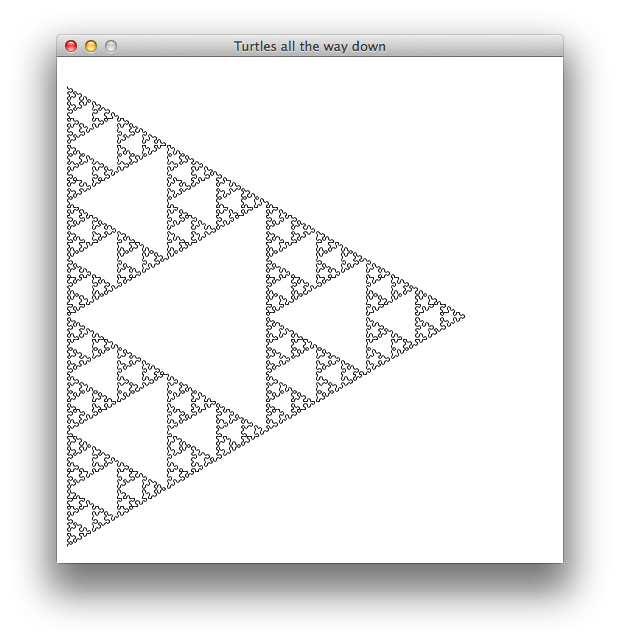
Line length: 0.9 — Depth: 9
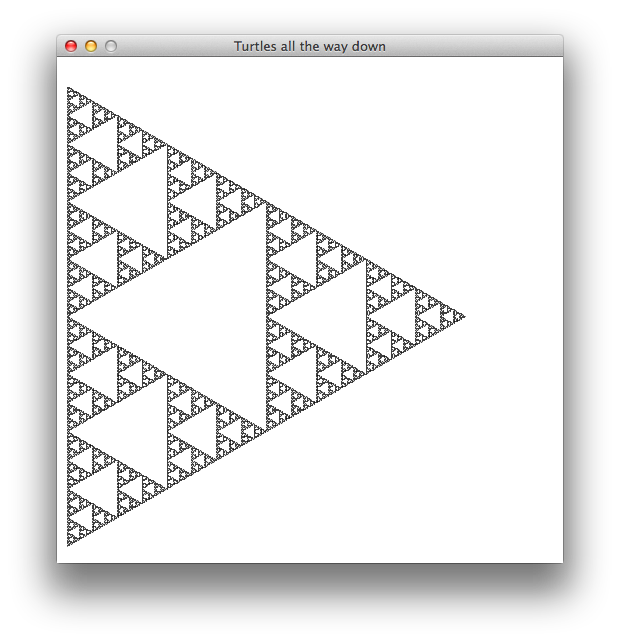
To explain how you can make these pictures, let's take a closer look at the depth 5 image:
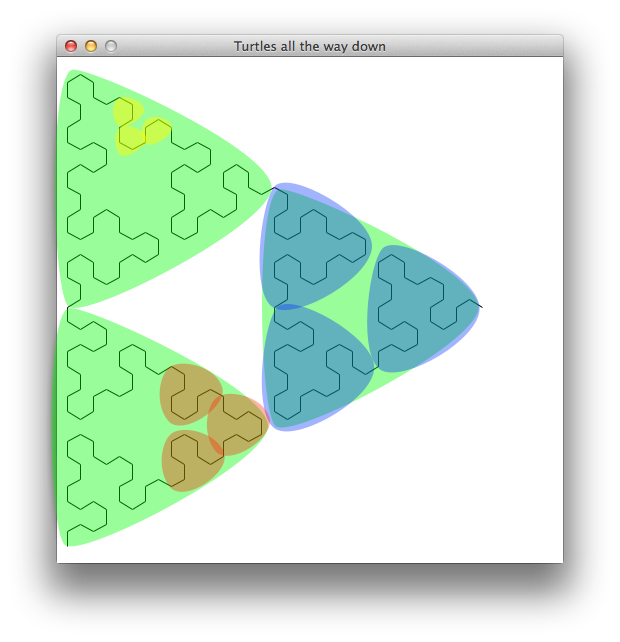
Notice that the whole image is composed of three pieces (highlighted in green) which are identical, except for their position and rotation. Each of the green triangles is itself composed of three smaller triangles (highlighted in blue). Each of the blue triangles is composed of three smaller "triangles" (highlighted in red). Even the little red triangles are composed of three individual lines (highlighted in yellow) that follow the same pattern.
This pattern suggests strongly that your triangle function should make three recursive calls, where each call reduces the nesting depth.
Between recursive calls, the turtle has to make a 60° turn to the left or a 60° turn to the right (which is the same as a -60° turn to the left). This can be seen most clearly at the lowest depth (highlighted in yellow).
The final tricky bit is that some of the recursive calls need to flip whether the turning should be to the left or to the right.
Putting this all together, drawing a triangle with turtle graphics goes something like this:
- If depth is zero, draw a straight line.
- Else (depth is greater than zero) ...
- Draw a triangle of one less depth with the reverse angle.
- Turn by the current angle.
- Draw a triangle of one less depth with the current angle.
- Turn by the current angle.
- Draw a triangle of one less depth with the reverse angle.
Python has a rich library of file information from os.path. Take a look at the documentation and see if you can list all the files that were modified after a specified time.
The drawings you did a examples of a general idea called L-systems. Write a program that can read more general L-system descriptions and draw them. You might find some good inspiration here.
You may run handin21 as many times as you like, and only the
most recent submission will be recorded. This is useful if you realize,
after handing in some programs, that you'd like to make a few more
changes to them.