CS21 Lab 10: recursion
This week we will write a variety of smaller programs to practice using recursion.
Run update21, if you haven't already, to create the cs21/labs/10 directory. Then cd into your cs21/labs/10 directory and create the python programs for lab 10 in this directory (handin21 looks for your lab 10 assignments in your cs21/labs/10 directory).
$ update21 $ cd cs21/labs/10
You will save your work for just this question in a file called xerox.py
Write a function called xerox that has two parameters: an item (could be anything) and a number n. Your function should use recursion to generate and return a python list containing n copies of the item. If n is zero, xerox returns an empty list. Here are some examples:
- xerox("paper", 4) returns:
['paper', 'paper', 'paper', 'paper'] - xerox(2, 10) returns:
[2, 2, 2, 2, 2, 2, 2, 2, 2, 2]
Add a main() function to your file to test out at least 4 different calls to the xerox() function.
xerox hint: you can add lists together in python:
>>> print L1 ['paper', 'paper', 'paper'] >>> print L2 ['pony', 'pony'] >>> print L1 + L2 ['paper', 'paper', 'paper', 'pony', 'pony']
You will save your work for just this question in a file called replace.py
Write a function called replace that has three parameters: text, ch, and newstr, which are all strings. You function should use recursion to replace each occurence of ch in text with newstr. For example, calling replace("abcdefg", "c", "PONY") would return "abPONYdefg". Here are some more examples:
- replace("abcde","c","123") returns:
'ab123de' - replace("12341234", "2", "999") returns:
'199934199934' - replace("F-F-F-F", "F", "F+F") returns:
'F+F-F+F-F+F-F+F'
Add a main() function to your file to test out at least
4 different calls to the replace() function. You should assume that
ch will always be a single character (a string of length 1).
Python comes with a built-in graphics package called turtle graphics (imagine a turtle walking on the beach, dragging it's tail). Here is a sample code to see how it works.
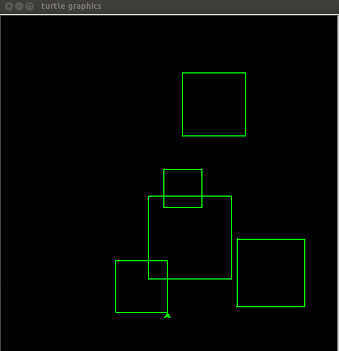
Write a program called squares.py that uses turtle graphics to draw 5 random-sized squares at random locations in the graphics window. Your program should include a function (drawSquare()) that draws a square, given a turtle, the x,y coordinates of a point (the center of the square), and a size (the length of the side of a square) as parameters.
NOTE: in turtle graphics,
the point 0,0 is at the center of the screen (unlike Zelle graphics).
Write a function (drawCodestring()) that has 4 parameters: a codestring, a turtle, a line size, and an angle. NOTE: this could be but is not intended to be a recursive function -- it is fine if you just use a simple for loop for this one! Your function should use turtle graphics to draw whatever commands it is given in the codestring, based on the following symbols:
- F = go forward/draw (amount = line size)
- + = turn right (angle)
- - = turn left (angle)
- [ = save state (position and heading of turtle)
- ] = restore state (position and heading of turtle)
Here are some sample codestrings and what they would draw:
F-F-F-F draws a square if angle is 90
F+F+F draws a triangle if angle is 120
F-F++F-F draws a line with a bump in it if angle is 60
F[-F]+F draws a Y if angle is small, like 45 or less
(try it on paper if you don't understand this one!)
F[-F]F[+F][F] draws a small twig-like set of lines (if angle = 25)
You can think of "saving the state of the turtle" as dropping a breadcrumb, where the breadcrumb remembers the position and the heading of the turtle. One way to save and restore the state of the turtle is by appending to and popping from a python list. For example:
state = [] # save state pos = turtle.position() head = turtle.heading() state.append([head, pos]) # restore state head,pos = state.pop() turtle.setposition(pos) turtle.setheading(head)
Add a main() function to test your codestring-drawing function.
Make sure the above examples all work.
L-systems have been used to model growth in complex organisms and biological systems. A typical L-system has an initial "start" string and a production rule to apply to the start string. Repeatedly applying the production rule to the resulting output leads to interesting patterns.
For example, suppose the initial start string is "F" and the production rule is "replace every F with F-F++F-F". Applying the rule 3 times leads to this:
0 F 1 F-F++F-F 2 F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F 3 F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F-F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F-F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F
If we use your drawCodestring() function above, with an angle of 60, this set of strings produce what are called Koch Curves. Here are the Koch curves for the first 4 applications of the following production rule:
Start: F
Rule: F --> F-F++F-F
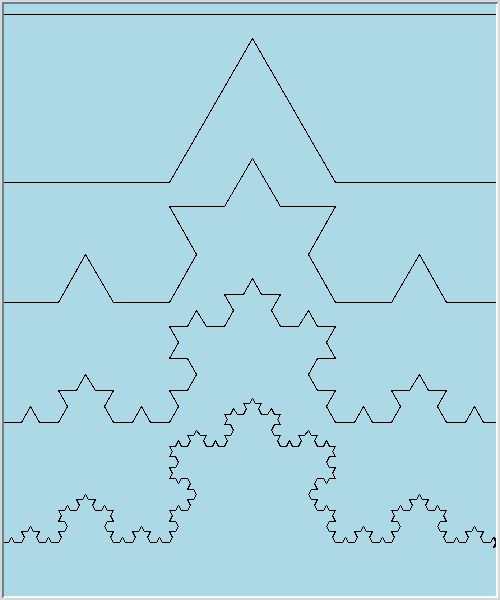
Add some code to your L-systems.py file to draw a Koch Curve: ask the user how many times to apply the production rule (num2apply), call your replace() function (num2apply times) to generate the appropriate codestring, then call drawCodestring() with the appropriate line size and angle to draw the curve.
To make the drawing fit in the graphics window, no matter what the user enters for num2apply, use a line size as follows:
line_size = float(turtle.window_width()) / (3**num2apply)(line size gets smaller as user asks for larger num2apply)
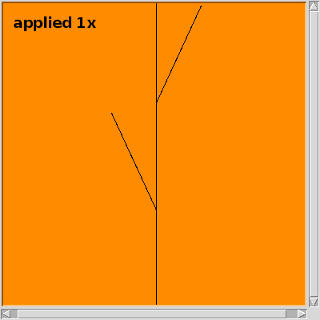
Many interesting and life-like patters can be created with L-systems. Here is another production rule:
Start: F
Rule: F --> F[-F]F[+F][F]
Using an angle of 25 degrees and a line size as follows:
line_size = float(turtle.window_height()) / (2**(num2apply+1)-1)
should produce a drawing similar to a bush or shrub (see below). Add some code to your L-systems.py file to draw a shrub based on the above rule and how many times the user wants to apply that rule.
Change your main program to first ask if they want to draw a Koch curve or a shrub, then ask the user how many times to apply the production rule.



- For high levels of recursion, drawing using turtle graphics can be
S-L-O-W. Add the following tracer() and update()
methods to your code to speed things up:
w = 800 h = w turtle.setup(width=w, height=h) gw = turtle.Screen() larry = turtle.Turtle() larry.tracer(50,0) # add this!! larry.hideturtle() # add this!! # draw stuff here, using larry # draw stuff here, using larry turtle.update() # add this (after drawing commands)!! gw.exitonclick()
- python has a "maximum recursion depth limit" set to 1000. If your program exceeds
this depth, it will crash. If you need to increase the depth limit, try this:
import sys sys.setrecursionlimit(2000)
- draw a Koch "snowflake" using 3 Koch Curves that form a triangle

- add some randomness and leaves (dots) to make the shrub more realistic

- create a scene with lots of random shrubs, grass, clouds, and the sun
- try some other L-systems
(Trees? Sierpinski triangle? Penrose tiles? etc...) like this one:
Start: F-F-F-F-F (a pentagon, if angle is 72) Rule: F --> F-F++F+F-F-F
Once you are satisfied with your programs, hand them in by typing handin21 in a terminal window.