Lab 12: Turtles and Fractals
A skeleton version of the program will appear when you run update21 in a terminal window. The program handin21 will only submit files in this directory.
Some of the problems will have optional components that allow you to
further practice your skills in Python. Optional portions will not be
graded, but may be interesting for those wanting some extra challenges.
- window - The graphics window containing the turtle.
- width - The width of the graphics window.
- height - The height of the graphics window.
- xPos - The horizontal location of the turtle.
- yPos - The vertical location of the turtle.
- direction - The direction the turtle is heading, measured in degrees counter-clockwise from East: East is 0 degrees, North is 90 degrees, West is 180 degrees and South is 270 degrees.
- tailDown - A Boolean flag that is True if the turtle's tail is lowered.
Begin by implementing the constructor and string methods:
- The __init__ method should...
- ...take two parameters indicating the width and height of the turtle graphics window.
- ...create a new GraphWin object using the graphics class. The center of the graphics window should be (0,0) meaning that the lower left and upper right corners of the window should have coordinates (-width/2.0, -height/2.0) and (width/2.0, height/2.0), respectively. You can use the setCoords method on GraphWin objects to set up this coordinate system.
- ...place the turtle in the center of the window facing East (direction=0) with the turtle's tail down (in drawing mode).
- The __str__ method should return the status of a turtle
object as a string. For example, after creating a turtle, the status
would appear as follows:
Position: (0, 0) Direction: 0 degrees Tail down? True
To change or query the turtle's state, you can use a number of Turtle methods:
-
The following methods operate on the Turtle's position. Remember that
when the turtle's tail is down, it should draw a line in the window as
it moves.
- forward(dist) - Move the turtle forward by the given
dist in the direction the turtle is currently heading.
To do this you will need to move the turtle from its current
location (x1,y1) to a new location (x2, y2).
If the current turtle heading is dir, then the
location of (x2, y2) is given by the following equations:
x2 = x1 + dist*cos(dir) y2 = y1 + dist*sin(dir)
where dir is measured in radians. To convert from degrees to radians, use the radians function in the math library. - goto(x,y) - Move (in a straight line) to the location specified by the point (x, y). This does not change the direction that the turtle is facing.
- position() - Return the (x,y) location of the turtle as a tuple.
- right(angle) - Turn angle degrees to the right (clockwise). If the turtle is facing North, then right(90) would make the turtle face East while right(270) from North would make the turtle face West.
- left(angle) - Turn angle degrees to the left (counter-clockwise). If the turtle is facing North, then left(90) would make the turtle face West while left(270) from North would make the turtle face East.
- heading() - Return the angle the turtle is heading.
- up() - Raise the turtle's tail and stop drawing.
- down() - Lower the turtle's tail and start drawing.
- window_height() - Return the height of the graphics window.
- window_width() - Return the width of the graphics window.
- done() - Done drawing - wait for a mouse click and close the window.
These methods operate on the Turtle's direction:
These methods operate on the Turtle's pen:
These methods operate on the Turtle's graphics window:
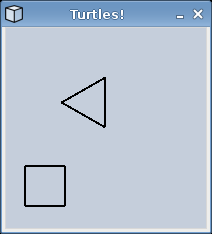
Below is the code that was used to create this image:
trevor = Turtle(200, 200) # at (0,0) facing East
trevor.left(90) # turn left 90 degrees (now facing North)
# A triangle
for i in range(3):
trevor.forward(50) # move forward 50 steps
trevor.left(120) # turn left 120 degrees
trevor.up() #stop drawing
trevor.goto(-80,-80) #go to (-80, 80)
trevor.down() #resume drawing
# A square
for i in range(4):
trevor.forward(40) # move forward 40 steps
trevor.right(90) # turn right 90 degrees
trevor.done() # wait for mouse click to close window
You can also test your Turtle class with the drawHouse
function that is included in the turtle.py file. Be sure to
test the Turtle class on these examples before implementing the
fractals described below.
The Koch curve is recursively defined:
- A Koch curve of level 0 is a line of the specified length.
- A Koch curve of level level is formed by four Koch curves as follows:
- drawing a Koch curve of length length/3.0 with level level-1
- turning 60 degrees to the left
- drawing a Koch curve of length length/3.0 with level level-1
- turning 120 degrees to the right
- drawing a Koch curve of length length/3.0 with level level-1
- turning 60 degrees to the left
- drawing a Koch curve of length length/3.0 with level level-1
Write a function snowflake(turtle, sides, length, level) that can draw a Koch snowflake, as described on page 465-466. A Koch snowflake is formed by putting together multiple copies of the Koch curve. The snowflake function is not a method of the Turtle class.
The algorithm for drawing a Koch snowflake with n sides is:
for each side: draw a Koch curve of the appropriate length and level turn right 360.0/n degreesThe snowflake shown below is an example of a Koch snowflake made with three Koch curves.

- Add a method backward(dist) which moves the turtle backward dist steps in the direction the turtle is currently facing.
- Add a method color(name) which sets the pen color using the color name specified. The default color is "black".
- Add a method width(w) which sets the thickness of the line drawn by the turtle to w.
- Add a method setHeading(angle) which sets the orientation of the turtle to angle.
- Add a method tracer(flag) which toggles whether or not a "turtle" is drawn on the screen showing its position and orientation. Rotating the turtle can be rather tricky, but if you use methods similar to the rotateBug and animateBug from homework 4, it can be done. Your turtle could be something simple like an filled arrow.
- Write a function cCurve(turtle, length, level) which draws a
c-Curve, as described on page 466-467. See the text for an example
picture. The cCurve function is not a method of the Turtle
class.
C-curves are defined recursively:
- A c-Curve of level 0 is a line of length length.
- A c-Curve of level level is formed as follows:
- turning 45 degrees to the left
- drawing a c-Curve of length length / sqrt(2) with level level-1
- turning 90 degrees to the right
- drawing a c-Curve of length length / sqrt(2) with level level-1
- turning 45 degrees to the left
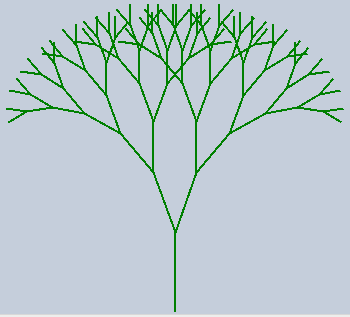
- Recursive techniques can be used to draw trees, ferns, and other patterns. The tree below is drawn by drawing the trunk, turning slightly to the left and recursively drawing a tree, then turning slightly right and recursively drawing a tree. Experiment with recursive drawing and come up with your own patterns.
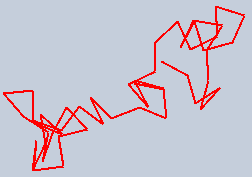
- Simulate a random walk by having the turtle repeatedly turning in a random direction and moving a small distance. An example random walk may look like this:
Once you are satisfied with your program, hand it in by typing handin21 in a terminal window.