
Your group should be based on the partner request form, and you should have a github repo ready to go by the time lab starts. Please let the instructor know if you have any issues accessing it.
The objectives of this lab are to:
The main steps of this lab are:
You will modify the following files:
You will use, but not modify, our implementation of neural networks from Lab 6, which is called neural_net.py. The Network class has been updated with two additional methods getWeights() and setWeights() to facilitate using neural networks within a genetic algorithm.
Open the file ga.py. You have been given a skeleton definition of the GeneticAlgorithm class that you will complete. Read through the methods that you will need to implement. Notice that the last two methods, called fitness and isDone, will not be implemented here. Instead they must be inherited and overridden.
Open up the file sum_ga.py. This contains an example class that overrides these methods. As you implement methods in the GeneticAlgorithm class, you will call them in the main program of this file to ensure that they are working as expected. Build your implementation incrementally, testing each new set of methods as you go.
To test them, modify the main program in the file sum_ga.py. Create an instance of the SumGA class where the length of the candidate solutions is 10 and the population size is 20. Use this instance to call the methods that you implemented. Next, add a for loop to print out each member of the population, and its fitness. Finally, print out the class variables you created to track the best ever fitness and best ever candidate solution. Ensure that they have been set correctly based on your initial population. To execute your test code do:
python3 sum_ga.py
Here is pseudocode for one algorithm achieving this:
spin = random() * totalFitness
partialFitness = 0
loop over the popSize
partialFitness += scores[i]
if partialFitness >= spin:
break
return a COPY of individual[i]
NOTE: there are more efficient algorithms for doing selection multiple times in a row; there are also library functions for doing this, like the ones we used for implementing stochastic beam search. For this lab, you are expected to implement your own, but you are allowed to use the simple, inefficient version given here.
Test that selection is working correctly. Use a loop to select popSize members of the population. Compute the total fitness of these newly selected members and compare that to the total fitness you found in the intial population. The new total should be higher.
0 1 2 3 4 5 6 7
parent1: [1, 1, 1, 0, 0, 0, 0, 0]
parent2: [0, 1, 0, 1, 0, 1, 0, 1]
^
crossPoint: 3
child1: [1, 1, 1, 1, 0, 1, 0, 1]
child2: [0, 1, 0, 0, 0, 0, 0, 0]
Test that your crossover method is working properly by printing out
the parents, the crossover point, and the resulting children.
child before mutation: [1, 1, 1, 1, 0, 1, 0, 1] child after mutation: [1, 0, 1, 1, 0, 1, 1, 1]Because the child is represented as a list, any change you make will be permanent, so this method does not need to return anything.
initialize the newPopulation to an empty list loop until the size of newPopulation >= the desired popSize select two parents apply crossover to these parents to generate two children mutate both children add both children to the newPopulation if size of newPopulation is > desired popSize slice out the last member of the newPopulation population = newPopulation
Test this method and see if the average fitness of the next population is higher than the average fitness of the previous population.
set class variables given in parameters
initialize a random population
evaluate the population
loop over max generations
run one generation
evaluate the population
if done
break
return the best ever individual
def main():
# Chromosomes of length 20, population of size 50
ga = SumGA(20, 50)
# Evolve for 100 generations
# High prob of crossover, low prob of mutation
bestFound = ga.evolve(100, 0.6, 0.01)
print(bestFound)
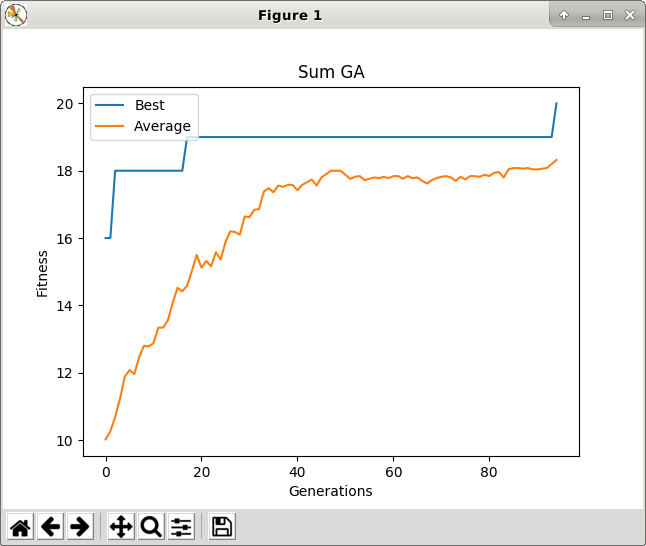
ga.plotStats("Sum GA")
Once you are convinced that the genetic algorithm is working properly, you will then move on to creating a specialized genetic algorithm that can evolve the weights and biases of a neural network.
Open the file neural_ga.py. This class is a specialization of the basic GeneticAlgorithm class. Rather than creating chromosomes of bits, it creates chromosomes of neural network weights (floating point numbers). There are only two methods you need to re-implement: initalizePopulation and mutate.
There is some test code provided that creates a population of size 5 of a small neural network with an input layer of size 2, an output layer of size 1, and no hidden layers. To execute this test code do:
python3 neural_ga.py
You should see that each chromosome contains small random weights and
that about 30 percent of the weights get mutated to new small random
weights.
Once this is working, you are ready apply your NeuralGA class to a reinforcement learnng problem.
In Lab 8, we used approximate Q-learning to solve the Cart Pole problem. We accomplished this by approximating the Q-learning table with a neural network. The inputs to the neural network were the states of the problem and the outputs were the estimated Q-values of doing each action in the given state. We applied back-propagataion to learn the weights, using the Q-learning update rule to generate targets for training.
Now that you have implemented GAs, we can tackle sequential decision problems in a new way. We will again use a neural network to represent the solution. Like before, the inputs to the network will represent the states of the problem, but now the outputs will represent the actions directly. Our goal will be to find a set of weights for the network such that the total reward received when following its action outputs is maximized. We will accomplish this by generating a population of random weight settings, and go through generations of selection, crossover, and mutation to find better and better weights. The fitness function will be the total reward received over an episode of choosing actions using the neural network.
The benefits of this approach over Q-learing are that now our actions need not be discrete, and our policy for behavior is much more direct--we are not learning values first, and then building a policy from them. We will compare the GA to Q-learning at solving the Cart Pole problem.
Open the file cartpole_neural_ga.py and complete the methods fitness and isDone. Here is pseudocode for the fitness method:
create a neural network with the appropriate layer sizes
if in 'testing' mode (i.e. passed a filename, not a chromosome)
set the weights of the network using the file
else
set the weights of the network using the chromosome
state, _ = reset the env
initialize total_reward to 0
loop over steps
when render is True, render the env
get the network's output from predicting the current state
choose action with max output value (hint: use np.argmax)
step the environment using that action saving the result
get the state, reward, and done from the result
update total_reward using the current reward
when done, break from the loop
if total_reward > bestEverScore
save network weights to a file
return total_reward
In order to use OpenAI Gym you'll need to activate the CS63 virtual environment:
source /usr/swat/bin/CS63env
To run the code do:
python3 cartpole_neural_ga.py
You should find that the GA can fairly quickly discover a set of weights that solve the Cart Pole problem.
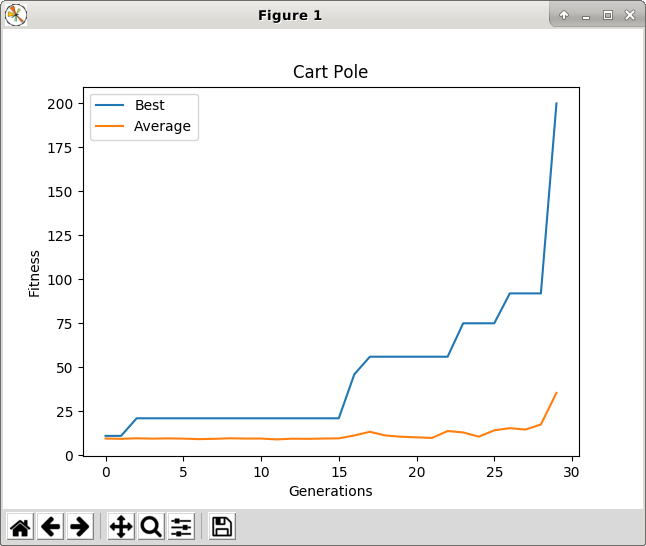
The cart pole GA should save the neural network weights associated with the best ever chromosome found in a file called bestEver.wts. To test out these weights do:
python3 testBest.py
This will render the cart pole environment and you should see that the pole is balanced for all 200 steps. There is some randomness in the testing, so some tests may not make it all the way until the end.