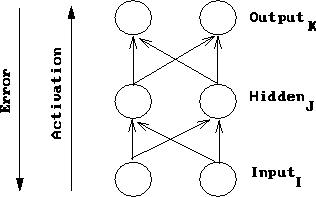
Figure 1: Neural network processing: Activation foward propagates and then error backward propagates. Weights on the connections mediate the passed values in both directions.
Figure 1 shows conceptually how network processing takes place.

Figure 1: Neural network processing: Activation foward propagates and
then error backward propagates. Weights on the connections mediate
the passed values in both directions.
Figure 2 depicts the network components which affect a particular weight change. Notice that all the necessary components are locally related to the weight being updated. This is one feature of backpropagation that seems biologically plausible. However, brain connections appear to be unidirectional and not bidirectional as would be required to implement backpropagation.
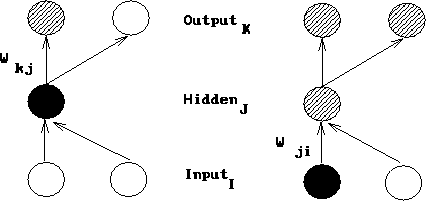
Figure 2: The change to a hidden to output weight depends
on error (depicted as a lined pattern) at the output node and
activation (depicted as a solid pattern) at the hidden node. While
the change to a input to hidden weight depends on error at the hidden
node (which in turn depends on error at all the output nodes) and
activation at the input node.
![]()
![]()
![]()
We can motivate the backpropagation learning algorithm as gradient
descent on sum-squared error (we square the error because we are
interested in its magnitude and not its sign). The total error in a
network is given by the following equation (the ![]() will
simplify things later).
will
simplify things later).
![]()
We want to adjust the network's weights to reduce this overall error.
![]()
We will begin at the output layer with a particular weight.
![]()
However error is not directly a function of a weight. We expand this as follows.
![]()
Let's consider each of these partial derivatives in turn. Note that only one term of the E summation will have a non-zero derivative: the one associated with the particular weight we are considering.
![]()
Now we see why the ![]() in the E term was useful.
in the E term was useful.
![]()
Note that only one term of the net summation will have a non-zero derivative: again the one associated with the particular weight we are considering.
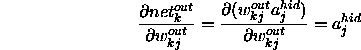
Now substituting these results back into our original equation we have:
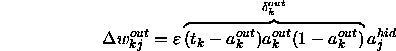
This is typically simplified as shown below where the ![]() term
repesents the product of the error with the derivative of the
activation function.
term
repesents the product of the error with the derivative of the
activation function.
![]()
Now we have to determine the appropriate weight change for an input to hidden weight.
![]()
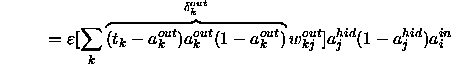
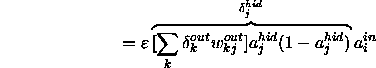
![]()