In this lab you will create simple CPPNs, which were introduced by Kenneth O. Stanley in the paper paper Compositional pattern producing networks: A novel abstraction for development.

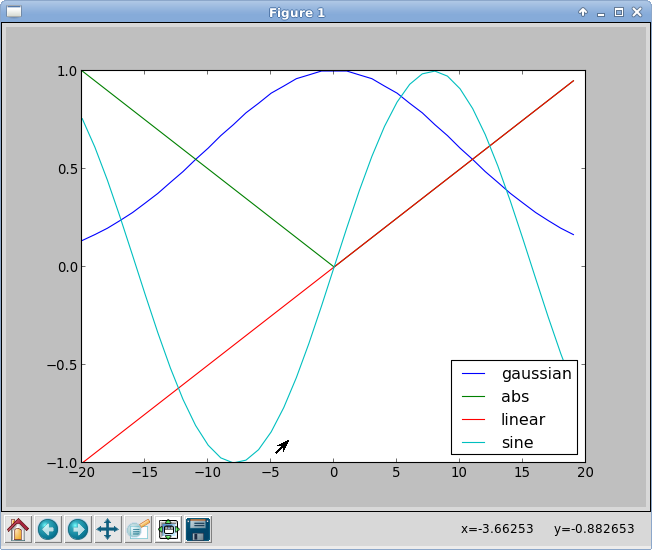
A CPPN is similar to an artificial neural network, except that at each node a different arbitrary function may be used in place of the typical sigmoid function. For example, functions such as gaussian, sine, linear, and absolute value could be used, as shown below.

Stanley argues that CPPNs can serve as a developmental encoding to map a genotype to a phenotype in an efficient way that doesn't depend on any local interaction. In his paper the genotype is a CPPN and the phenotype is an image generated from the CPPN. The inputs to the CPPN are:

• x: a x coordinate
• y: a y coordinate
• d: the distance d of the point (x, y) from the center of the image (0,0)
• bias: a constant input of 1.0

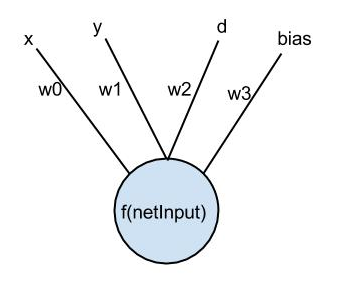
The simplest CPPN possible is one that has no hidden units (as shown below), where w0-w3 are weights in the range [-1,1], and the output of the network is a function of the weighted sum of the inputs.

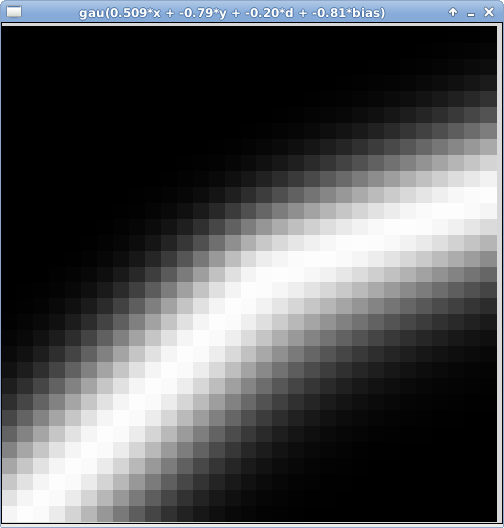
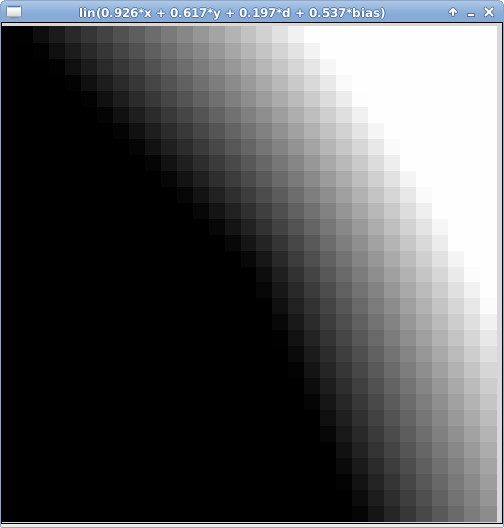
In this lab we will generate CPPNs with the structure above using random weights and a randomly chosen function, to explore the range and complexity of images that result. Even with this very simple structure, some surprisingly complex images can be produced. Below are some sample images.

Do an update81 to get the starting point files for this lab.

• drawPic.py This file contains a function called display that takes an n by n matrix of values in the range [0,1], and draws a grayscale image of those values.
• cppn.py This is where you will write your solution to the lab.

Execute the drawPic.py file. You will use the display function as a helper in your implementation.

1. Create a constructor that takes a dimension for the matrix as a parameter. Represent the matrix as a list of lists, where each inner list is a row. It should initialize the matrix to contain all 0's.

2. Create a distance method that takes two points and returns the distance between them.

3. Create one method for each possible type of function you want to include in your CPPN. Each method should take a value, and apply the function to that value to generate an output. At a minimum you should include methods for the four functions mentioned above (linear, absolute value, sine, and gaussian). For the linear and absolute value functions, divide the outputs by half of the dimension of the matrix. For sine, multiply the input by a quarter of the dimension of the matrix. You can find the equation for a gaussian function on wikipedia; it takes four parameters, which I set as follows a=1, b=0, c=3, and d=0.

4. Create a method to generate an instance of the simple CPPN shown previously, which has no hidden units. You will need to generate four random weights and one random function (from the choices you implemented in the previous step). Use the pseudo code below to generate a matrix of values that you can pass to the display helper function to visualize the result.

   for row in range(dimension)
      y = row - dimension/2
      for col in range(dimension)
         x = col - dimension/2
         d = distance( (x, y), (0, 0) )
         netInput = weighted sum of the inputs x, y, d, and bias
         output = function(netInput)
         if output > 1 set to 1
         if output < 0 set to 0
         matrix[row][col] = output
   display the matrix with a title that describes all of the relevant parameters
   

5. Your main program should create an instance of the class, and then call the method that generates a simple CPPN.

Run handin81 before the due date to turn in your lab.