
In this project, you will implement value iteration and q-learning. You will test your agents first on Gridworld, then apply them to a simulated robot controller (Crawler) and Pac-Man.
The code for this project contains the following files, which will be copied to your directory when you run update63.
valueIterationAgents.py |
A value iteration agent for solving known MDPs. |
qlearningAgents.py |
Q-learning agents for Gridworld, Crawler and Pac-Man. |
analysis.py |
A file to put your answers to questions given in the project. |
mdp.py |
Defines methods on general MDPs. |
learningAgents.py |
Defines the base classes ValueEstimationAgent and QLearningAgent, which your agents will extend. |
util.py |
Utilities, including util.Counter, which is particularly useful for q-learners. |
gridworld.py |
The Gridworld implementation. |
featureExtractors.py |
Classes for extracting features on (state,action) pairs. Used for the approximate q-learning agent (in qlearningAgents.py). |
environment.py |
Abstract class for general reinforcement learning environments. Used
by gridworld.py. |
graphicsGridworldDisplay.py |
Gridworld graphical display. |
graphicsUtils.py
|
Graphics utilities. |
textGridworldDisplay.py |
Plug-in for the Gridworld text interface. |
crawler.py |
The crawler code and test harness. You will run this but not edit it. |
graphicsCrawlerDisplay.py |
GUI for the crawler robot. |
Your code will be autograded for technical correctness. Please do not change the names of any provided functions or classes within the code, or you will wreak havoc on the autograder. However, the correctness of your implementation (not the autograder's judgements) will be the final judge of your score. If necessary, we will review and grade assignments individually to ensure that you receive due credit for your work.
In this project there are 9 required questions worth a possible 22 points.
To get started, run Gridworld in manual control mode, which uses the arrow keys:
python gridworld.py -m
You will see the two-exit layout from class. The blue dot is the agent. Note that when you press the up arrow key, the agent only actually moves north 80% of the time. Such is the life of a Gridworld agent!
You can control many aspects of the simulation. A full list of options is available by running:
python gridworld.py -h
The default agent moves randomly
python gridworld.py -g MazeGrid
You should see the random agent bounce around the grid until it happens upon an exit. Not the finest hour for an AI agent.
Note: The Gridworld MDP is such that you first must enter a pre-terminal state (the double boxes shown in the GUI) and then take the special 'exit' action before the episode actually ends (in the true terminal state called TERMINAL_STATE, which is not shown in the GUI). If you run an episode manually, your total return may be less than you expected, due to the discount rate (-d to change; 0.9 by default).
Look at the console output that accompanies the graphical output (or use -t for all text).
You will be told about each transition the agent experiences (to turn this off, use -q).
As in Pac-Man, positions are represented by (x,y)
Cartesian coordinates and any arrays are indexed
by [x][y], with 'north' being the
direction of increasing y, etc. By default, most
transitions will receive a reward of zero, though you can change
this with the living reward option (-r).
Question 1 (3 points) Write a
value iteration agent in ValueIterationAgent, which has
been partially specified for you
in valueIterationAgents.py. Your value iteration
agent is an offline planner, not a reinforcement agent, and so the
relevant training option is the number of iterations of value
iteration it should run (option -i) in its initial
planning phase.
The ValueIterationAgent takes an MDP on construction
and runs value iteration for the specified number of iterations before
the constructor returns. Use the "batch" version of value iteration
where each set of values is computed from the fixed previsous set of
values (like the pseudocode presented in lecture). Remember that you
have access to all of the lecture material in
your cs63/lectures/ directory. You will also write the
method getPolicy that uses the utility values to generate
a policy.
The following command loads your ValueIterationAgent, which will compute a policy and execute it 10 times. After value iteration is complete, press a key to start the simulation. You should find that the value of the start state (V(start)) and the empirical resulting average reward are quite close.
python gridworld.py -a value -i 100 -k 10
Hint: On the default BookGrid, running value iteration for 5 iterations should give you this output:
python gridworld.py -a value -i 5
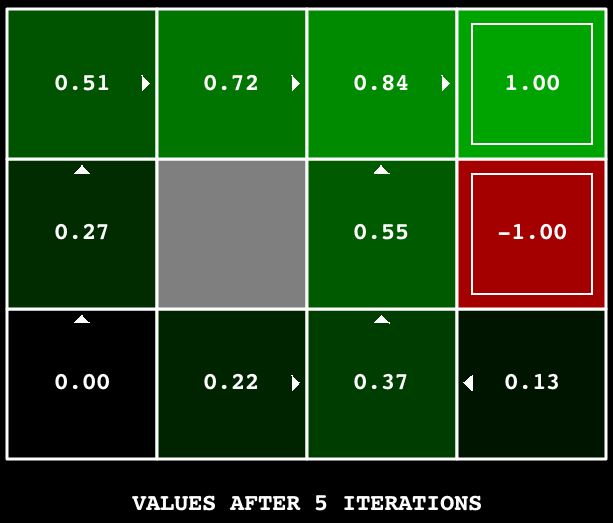
Your value iteration agent will be graded on a new grid. We will check your values and policies after fixed numbers of iterations and at convergence (e.g. after 100 iterations).
Hint: Use the util.Counter class in util.py, which is a dictionary with a default value of zero.
Question 2 (1 point) On BridgeGrid with the default discount of 0.9 and the default noise of 0.2, the optimal policy does not cross the bridge.
Change only ONE of the discount and noise parameters so that the optimal policy causes the agent to attempt to cross the bridge. Put your answer in question2() of analysis.py. (Noise refers to how often an agent ends up in an unintended successor state when they perform an action.) The default corresponds to:
python gridworld.py -a value -i 100 -g BridgeGrid --discount 0.9 --noise 0.2
Question 3 (5 points) Consider
the DiscountGrid layout, shown below. This grid has two
terminal states with positive payoff (shown in green), a close exit
with payoff +1 and a distant exit with payoff +10. The bottom row of
the grid consists of terminal states with negative payoff (shown in
red); each state in this "cliff" region has payoff -10. The starting
state is the yellow square. We distinguish between two types of
paths: (1) paths that "risk the cliff" and travel near the bottom
row of the grid; these paths are shorter but risk earning a large
negative payoff, and are represented by the red arrow in the figure
below. (2) paths that "avoid the cliff" and travel along the top
edge of the grid. These paths are longer but are less likely to
incur huge negative payoffs. These paths are represented by the
green arrow in the figure below.
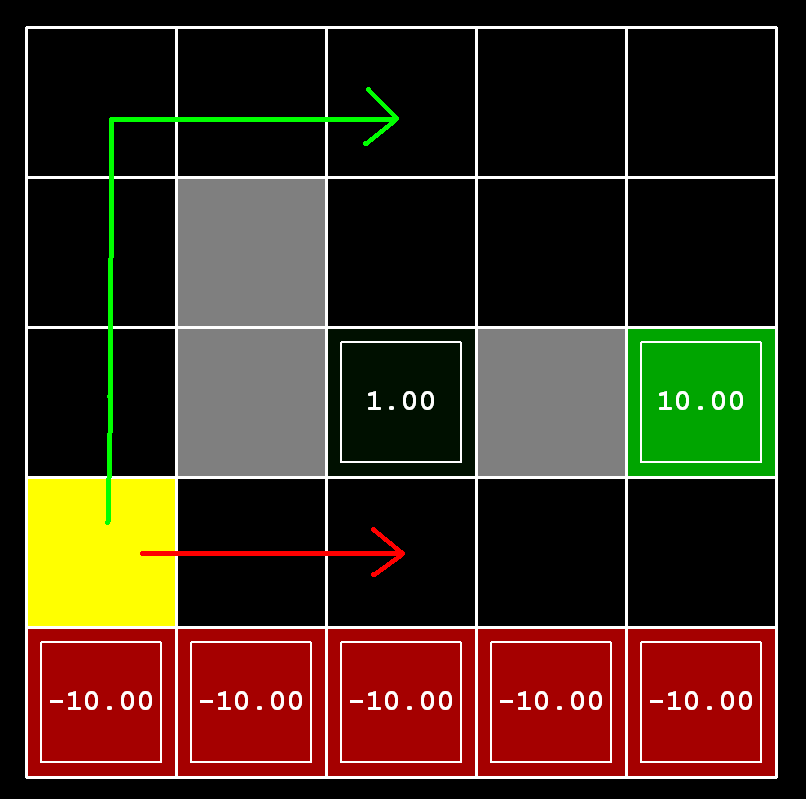
Give an assignment of parameter values for discount, noise, and
livingReward which produce the following optimal policy types or
state that the policy is impossible by returning the
string 'NOT POSSIBLE'. The default corresponds to:
python gridworld.py -a value -i 100 -g DiscountGrid --discount 0.9 --noise 0.2 --livingReward 0.0
question3a() through question3e() should each return a 3-item tuple of (discount, noise, living reward) in analysis.py.
Note: You can check your policies in the GUI. For example, using a correct answer to 3(a), the arrow in (0,1) should point east, the arrow in (1,1) should also point east, and the arrow in (2,1) should point north.
Note that your value iteration agent does not actually learn from experience. Rather, it ponders its MDP model to arrive at a complete policy before ever interacting with a real environment. When it does interact with the environment, it simply follows the precomputed policy (e.g. it becomes a reflex agent). This distinction may be subtle in a simulated environment like a Gridword, but it's very important in the real world, where the real MDP is not available.
Question 4 (5 points) You will now write
a q-learning agent, which does very little on construction, but
instead learns by trial and error from interactions with the
environment through its update(state, action, nextState,
reward) method. A stub of a q-learner is specified
in QLearningAgent in qlearningAgents.py, and
you can select it with the option '-a q'. For this
question, you must implement the
constructor, getQValue, computeValueFromQValues, computeActionFromQValues,
and update methods.
Note: For computeValueFromQValues and computeActionFromQValues, you should break ties randomly for better behavior. The random.choice() function will help. In a particular state, actions that your agent hasn't seen before still have a Q-value, specifically a Q-value of zero, and if all of the actions that your agent has seen before have a negative Q-value, then an unseen action may be optimal.
Important: Make sure that you only access Q values by calling
getQValue in
your methods. This
abstraction will be useful for question 9 when you
override getQValue to use features of state-action
pairs rather than state-action pairs directly.
With the q-learning update in place, you can watch your q-learner learn under manual control, using the keyboard:
python gridworld.py -a q -k 5 -mRecall that
-k will control the number of episodes your agent gets to learn.
Watch how the agent learns about the state it was just in, not the one it moves to, and "leaves learning in its wake."
Question 5 (2 points) Complete your q-learning agent by implementing epsilon-greedy action selection in getAction, meaning it chooses random actions epsilon of the time, and follows its current best q-values otherwise.
python gridworld.py -a q -k 100Your final q-values should resemble those of your value iteration agent, especially along well-traveled paths. However, your average returns will be lower because of the random actions and the initial learning phase.
You can choose an element from a list uniformly at random by calling the random.choice function.
You can simulate a binary variable with probability p
of success by using util.flipCoin(p), which returns True with
probability p and False with probability 1-p.
Question 6 (1 points) First, train a completely random q-learner with the default learning rate on the noiseless BridgeGrid for 50 episodes and observe whether it finds the optimal policy.
python gridworld.py -a q -k 50 -n 0 -g BridgeGrid -e 1Now try the same experiment with an epsilon of 0. Is there an epsilon and a learning rate for which it is highly likely (greater than 99%) that the optimal policy will be learned after 50 iterations?
question6() should return EITHER a 2-item tuple of (epsilon, learning rate) OR the string 'NOT POSSIBLE' if there is none. Epsilon is controlled by -e, learning rate by -l.
With no additional code, you should now be able to run a q-learning crawler robot:
python crawler.pyIf this doesn't work, you've probably written some code too specific to the
GridWorld problem and you should make it more general to all MDPs. You will receive full credit if the command above works without exceptions.
This will invoke the crawling robot from class using your q-learner. Play around with the various learning parameters to see how they affect the agent's policies and actions. Note that the step delay is a parameter of the simulation, whereas the learning rate and epsilon are parameters of your learning algorithm, and the discount factor is a property of the environment.
Question 7 (1 point) Time to play some
Pac-Man! Pac-Man will play games in two phases. In the first
phase, training, Pac-Man will begin to learn about the values
of positions and actions. Because it takes a very long time to learn
accurate q-values even for tiny grids, Pac-Man's training games run in
quiet mode by default, with no GUI (or console) display. Once
Pac-Man's training is complete, he will enter testing mode.
When testing, Pac-Man's self.epsilon
and self.alpha will be set to 0.0, effectively stopping
q-learning and disabling exploration, in order to allow Pac-Man to
exploit his learned policy. Test games are shown in the GUI by
default. Without any code changes you should be able to run
q-learning Pac-Man for very tiny grids as follows:
python pacman.py -p PacmanQAgent -x 2000 -n 2010 -l smallGridNote that
PacmanQAgent is already defined for you in
terms of the QLearningAgent you've already
written. PacmanQAgent is only different in that it has
default learning parameters that are more effective for the Pac-Man
problem (epsilon=0.05, alpha=0.2, gamma=0.8). You will
receive full credit for this question if the command above works
without exceptions and your agent wins at least 80% of the last 10
runs.
Hint: If your QLearningAgent works
for gridworld.py and crawler.py but does not
seem to be learning a good policy for Pac-Man
on smallGrid, it may be because
your getAction and/or getPolicy methods do
not in some cases properly consider unseen actions. In particular,
because unseen actions have by definition a Q-value of zero, if all of
the actions that have been seen have negative Q-values, an
unseen action may be optimal.
Note: If you want to experiment with learning parameters,
you can use the option -a, for
example -a epsilon=0.1,alpha=0.3,gamma=0.7. These
values will then be accessible as self.epsilon,
self.gamma and self.alpha inside the agent.
Note: While a total of 2010 games will be played, the
first 2000 games will not be displayed because of the option -x
2000, which designates the first 2000 games for training (no
output). Thus, you will only see Pac-Man play the last 10 of these
games. The number of training games is also passed to your agent as
the option numTraining.
Note: If you want to watch 10 training games to see what's going on, use the command:
python pacman.py -p PacmanQAgent -n 10 -l smallGrid -a numTraining=10During training, you will see output every 100 games with statistics about how Pac-Man is faring. Epsilon is positive during training, so Pac-Man will play poorly even after having learned a good policy: this is because he occasionally makes a random exploratory move into a ghost. As a benchmark, it should take about 1,000 games before Pac-Man's rewards for a 100 episode segment becomes positive, reflecting that he's started winning more than losing. By the end of training, it should remain positive and be fairly high (between 100 and 350).
Make sure you understand what is happening here: the MDP state is the exact board configuration facing Pac-Man, with the now complex transitions describing an entire ply of change to that state. The intermediate game configurations in which Pac-Man has moved but the ghosts have not replied are not MDP states, but are bundled in to the transitions.
Once Pac-Man is done training, he should win very reliably in test games (at least 90% of the time), since now he is exploiting his learned policy.
However, you'll find that training the same agent on the seemingly
simple mediumGrid may not work well. In our
implementation, Pac-Man's average training rewards remain negative
throughout training. At test time, he plays badly, probably losing
all of his test games. Training will also take a long time, despite
its ineffectiveness.
Pac-Man fails to win on larger layouts because each board configuration is a separate state with separate q-values. He has no way to generalize that running into a ghost is bad for all positions. Obviously, this approach will not scale.
Question 8 (3 points)
Implement an approximate q-learning agent that learns weights for features of states, where many states might share the same features. Write your implementation in ApproximateQAgent class in qlearningAgents.py, which is a subclass of PacmanQAgent.
Note: Approximate q-learning assumes the existence of a feature function f(s,a) over state and action pairs, which yields a vector f1(s,a) .. fi(s,a) .. fn(s,a) of feature values. We provide feature functions for you in featureExtractors.py. Feature vectors are util.Counter (like a dictionary) objects containing the non-zero pairs of features and values; all omitted features have value zero.
The approximate q-function takes the following form
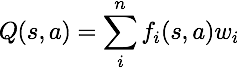
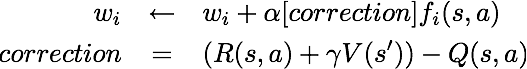
By default, ApproximateQAgent uses the IdentityExtractor, which assigns a single feature to every (state,action) pair. With this feature extractor, your approximate q-learning agent should work identically to PacmanQAgent. You can test this with the following command:
python pacman.py -p ApproximateQAgent -x 2000 -n 2010 -l smallGrid
Important: ApproximateQAgent is a subclass of QLearningAgent, and it therefore shares several methods like getAction. Make sure that your methods in QLearningAgent call getQValue instead of accessing q-values directly, so that when you override getQValue in your approximate agent, the new approximate q-values are used to compute actions.
Once you're confident that your approximate learner works correctly with the identity features, run your approximate q-learning agent with our custom feature extractor, which can learn to win with ease:
python pacman.py -p ApproximateQAgent -a extractor=SimpleExtractor -x 50 -n 60 -l mediumGrid
Question 9 (1 point)
Even much larger layouts should be no problem for your ApproximateQAgent. (warning: this may take a few minutes to train)
python pacman.py -p ApproximateQAgent -a extractor=SimpleExtractor -x 50 -n 60 -l mediumClassic
If you have no errors, your approximate q-learning agent should win almost every time with these simple features, even with only 50 training games.
You have completed Project 3. You have a learning Pac-Man agent!
Remember to run handin63 by 11:59pm on Tuesday,
Nov. 12. Also be sure to select your partner.