Lab9: Using recursion to create fractals
The goal of this program is to learn about recursion by designing fractal patterns. We will be using the graphics library that we used in Labs 4 & 5 again for this lab.
To start, run update21 to create the cs21/labs/09 directory containing two starting point files called pattern.py and tree.py. Edit these files to create your solutions for this lab.
You may work with a partner on this assignment. The best way to
work as a team is to sit together to design and to code your
solution. Take turns typing and watching. If you work with a partner,
put your name and the name of your partner in the list of authors at
the top of your program. Only one partner should run handin21
to submit the files for the group. Both partners will receive the same
grade.
A fractal is a seemingly complex pattern that is built up from many copies of some rather simple base pattern. Create a fractal of your own design using just one shape, such as a circle, a rectangle, or an oval.
Here is an example of a fractal that is built up from a repeating pattern of circles. This was created by recursively drawing four smaller circles around the center point of the current circle.
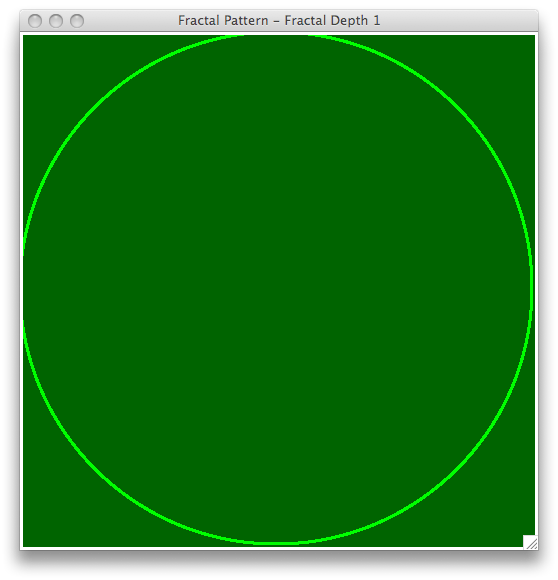



Use recursion to implement your own fractal pattern. Your program should include a function like the one shown below that takes a graphics window, an integer n representing the depth of the fractal, and any other parameters that you may need.
drawRecursivePattern(window, n, ...)
Recall that every recursive function needs a base case where the recursion ends. For drawing recrusive patterns the base case will occur when n is zero. Each recursive call should reduce n by one.
Your program should read in the value of n and draw the
pattern of the appropriate recursive depth.
Fractal patterns appear in many natural settings: tree branches, blood vessels, river networks, snow flakes, and crystals to name a few.
We will construct a fractal tree using recursion. Edit the program called tree.py. You will start by creating the tree trunk as one large branch. The trunk will then split into two big branches, each of which will split into two medium branches, and so on. Each final branch should end with a single leaf.
Here is an example of a fractal tree:
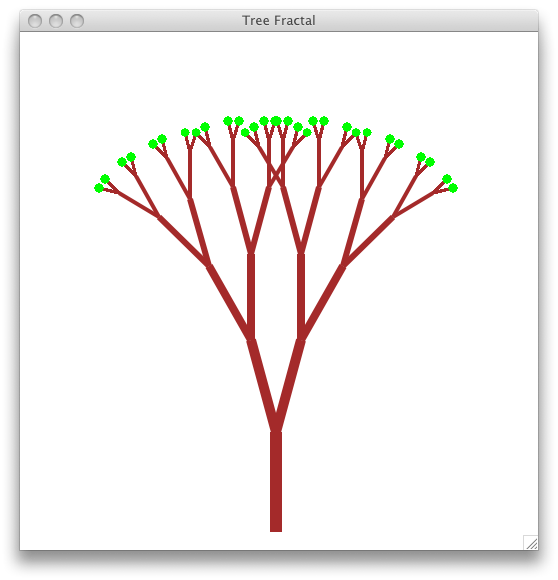
To create your tree, you will need three pieces of information from the user:
- n: recursive depth of tree (e.g., the number of branches between the trunk and a leaf.)
- splitAngle: the angle between two branches in each level of the tree (e.g., 30.0 degrees)
- scale: the relative length of a smaller branch relative to a bigger branch at each level in the tree. (e.g., 0.75 is a good scale factor).
You should write a recursive function called drawBranch that takes a graphics window, an integer n representing the current recursive depth, a start point for the current branch, an end point for the current branch, the angle in radians representing the orientation of the current branch, a float scale representing the relative length of smaller branches, and split an angle in radians between two branches at the same level in the tree:
drawBranch(window, n, start, end, angle, scale, split)
Note that, angle defines the orientation of the branch (in radians) where 0 radians is a horizonal line pointing to the left. As we move clockwise, this angle increases. As we move counter-clockwise, this angle decreases. The trunk of the tree is vertical and will have angle = -pi/2 (e.g., -90 degrees).
Remember that all angles should be in radians (except for the angle requested from the user, which should be in degrees). You can convert between degrees and radians using the radians() function in the math library.
To implement drawBranch you'll need to do the following:
- In the base case, draw a small green circle representing a leaf at the start point.
- In the other case:
- Draw the line defined by the start and end points. Set the width of the line based on n.
- Calculate the length of the current branch:
dx = end.getX() - start.getX() dy = end.getY() - start.getY() length = sqrt(dx**2 + dy**2)
- Use this length to determine the length of the new left and right branches, which will be based on the scale parameter.
- Each new branch will start at the end point of the current
branch, but will have unique end points. We can determine the end
point (x, y) of a new branch with the following formula:
x = end.getX() + length * cos(desiredAngle) y = end.getY() + length * sin(desiredAngle)
- To draw the tree you'll need to make a recursive call to drawBranch for the left branch and a recursive call drawBranch for the right branch. In these recurive calls the paramters window scale and split will remain unchanged. All of the other parameters will need to be modified.
Note: This is not required and should only be attempted once the previous two parts are working correctly. This problem is more difficult.
Below are examples of six Koch curves that have recursion depths from 0 (a straight line) at the top to 5 at the bottom.
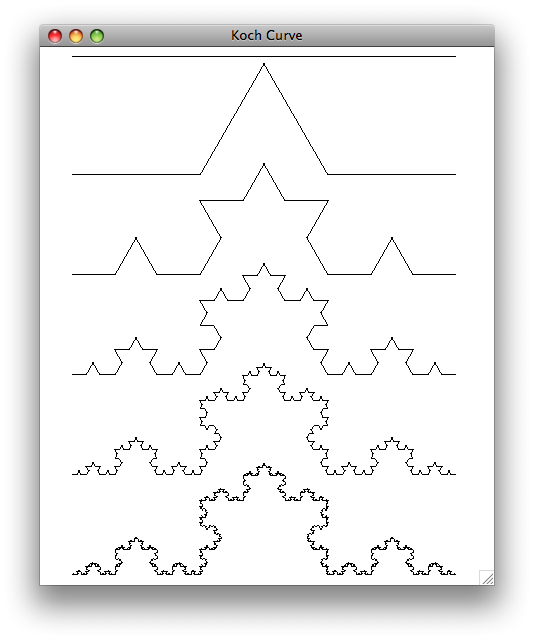
A Koch curve is created by breaking a line segment into thirds and replacing the middle segment by two segments that are equal in length. This creates a two-sided equilateral triangle in the middle (e.g., all angles are 60 degrees).
You should start by creating a program called koch.py. You will write a function:
drawKochCurve(win, n, start, end, angle)which draws a Koch curve from point start to a point end with recursion depth n where angle specfies the angle of the line that connects start to end.
A Koch curve of recursion depth n is formed by four Koch curves as follows:
- drawing a Koch curve of length length/3 with degree n-1 and angle
- drawing a Koch curve of length length/3 with degree n-1 and angle-radians(60)
- drawing a Koch curve of length length/3 with degree n-1 and angle+radians(60)
- drawing a Koch curve of length length/3 with degree n-1 and angle
Hint: Each one of these recursive calls is starting from a different starting point.
Once you have successfully create a single Koch curve, you can put three Koch curves to create a Koch snowflake. The snowflake shown below is an example of a Koch snowflake made with 3 Koch curves.
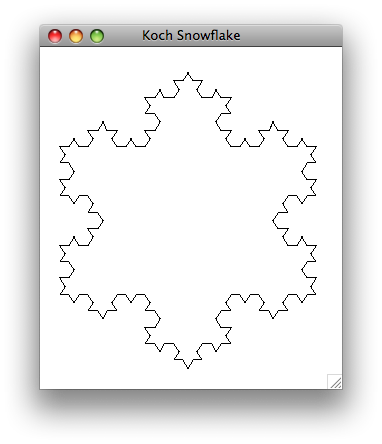
Once you are satisfied with your programs you can hand them in by typing handin21 in a terminal window.