CS21B Lab6: Population genetics
In this lab we will explore the topic of population genetics and consider how the proportion of genotypes within a population changes over time. A population is a group of organisms of the same species that can interbreed. In our simplified experiment, we will use organisms that contain a single gene. The alleles for this gene are 'T' and 't'. Each organism will get one allele from each parent. Organisms with the genotype 'TT', 'Tt', or 'tT' will be tall, and organisms with the genotype 'tt' will be short.
A skeleton version of the program population.py will appear
in your cs21/lab/06/ directory when you run update21
in a terminal window. The program handin21 will only submit
files in this directory.
Write a function called initializePopulation that takes as parameters,
- popSize: The size of the population represented as an integer.
- p: The probability of having the allele 'T' vs 't' represented as a floating point value between 0 and 1.
This function returns a list of organisms represented as strings.
Use the list method append to accumulate the population into a list. Use the random library function random() to do a biased coin flip based on the given probability p to determine whether each allele should be a 'T' or a 't'.
For example, calling initializePopulation(10, 0.5) will generate a list of ten organisms where approximately 50% of the alleles are 'T' and 50% are 't'.
['TT', 'tt', 'Tt', 'Tt', 'Tt', 'tt', 'tt', 'TT', 'TT', 'Tt']
Calling initializePopulation(10, 0.75) will generate a list of ten organisms where approximately 75% of the alleles are 'T' and 25% are 't'.
['tT', 'TT', 'TT', 'tT', 'tT', 'TT', 'TT', 'Tt', 'Tt', 'TT']
Calling initializePopulation(10, 0.25) will generate a list of ten organisms where approximately 25% of the alleles are 'T' and 75% are 't'.
['tt', 'tt', 'tt', 'tt', 'Tt', 'TT', 'tt', 'tt', 'tt', 'tt']
What should happen if the probability given to this funciton were 0 or 1? Test all of these cases in main before moving on to the next part.
Note that because the process of initializing a population is
random, it is unlikely that you will get the exact same results when
you test your code.
Write a function called countGenotypes that takes as a parameter,
- population: a list of organisms represented as strings
This function does not return anything.
The function should print the precentages of the dominant ('TT'), mixed ('Tt' or 'tT'), and recessive ('tt') genotypes in the given population. Use the list method count to help you compute the percentages.
For example, given the following population of 10 organisms:
['Tt', 'TT', 'tt', 'TT', 'tt', 'TT', 'Tt', 'tT', 'tt', 'tT']
3 out of 10 are dominant, 4 out of 10 are mixed, and 3 out of 10 are recessive. Therefore, countGenotypes function should print:
TT: 0.300 Tt and tT: 0.400 tt: 0.300
Test your function in main before moving on to the next part.
Write a function called oneGeneration that takes as a parameter,
- population: a list of organisms represented as strings
To create a child, randomly select two parents from the population. (Note that for the purposes of this simulation we are ignoring gender; any two organisms from the population are able to mate.) Then randomly select an allele from the first parent and randomly select an allele from the second parent. Combine these two alleles to make a child. For example, suppose that you randomly selected parent1 as 'TT' and parent2 as 'tt'. You would randomly select an allele from parent1: 'T' and randomly select an allele from parent2: 't' and form their child 'Tt'. Accumulate the children into a new population using the list append method.
You can use the choice function from the random library to make these random selections. Recall that if you have a list such as colors = ['red','blue','green'], then choice(colors) will select one of 'red', 'blue' or 'green' at random. Similarly, if you have a string such as s = 'rainbow', choice(s) will randomly select a letter from the string 'rainbow'.
Test your function in main before moving on to the next
part. Be sure that it returns a new population of the same size as
the original population. For example, oneGeneration(['TT', 'Tt',
'Tt', 'Tt', 'tt']) might return: ['tT', 'TT', 'Tt', 'Tt',
'Tt'].
Write a function called manyGenerations that takes as parameters,
- population: a list of organisms represented as strings
- numGenerations: the number of generations represented as an integer
Use the oneGeneration function that you wrote in the previous step to help you implement this function.
Test this function in your main program. Try creating an initial population of size 1000, using a probability of 0.5 for the 'T' allele. Use your countGenotypes function to summarize this initial population. You should see about 25% dominant, 50% mixed, and 25% recessive. Then try using your manyGenerations function on this initial population for 50 generations, and save the resulting population. Use your countGenotypes function to summarize this final population.
For example, your main should now be able to perform the following sort of interaction with the user:
Enter population size: 1000 Enter probability of 'T' allele in initial population: 0.5 Enter number of generations: 50 Initial distribution TT: 0.254 Tt and tT: 0.485 tt: 0.261 Final distribution TT: 0.224 Tt and tT: 0.487 tt: 0.289You should see that the proportion of each genotype is about the same. Try this multiple times. There will be significant variation using these relatively small numbers.
For a test with less variation try using a population of size 10000
and 200 generations. This may take 10 or more seconds to process.
Currently your program only reports the initial and final distribution of genotypes in the population. It would be nicer to graph the distribution across all the generations. To accomplish this, you'll need to update the manyGenerations function from the previous step.
Modify manyGenerations to accumulate three lists that maintain the counts of the genotypes (recessive, dominant, and mixed) for each generation. For example, suppose we were using populations of size 10. For each new generation, we would accumulate the counts of each kind of genotype as shown below. In generation 0, there were 4 recessive, 1 dominant, and 5 mixed. In generation 1, there were 4 recessive, 2 dominant, and 4 mixed. After simulating all of the generations, these three lists contain the history of counts for each kind of genotype in the population.
Generation: 0
Population: ['tt', 'tt', 'tT', 'tT', 'tT', 'tt', 'tT', 'tt', 'TT', 'Tt']
Recessive: [4]
Dominant: [1]
Mixed: [5]
Generation: 1
Population: ['Tt', 'TT', 'tt', 'Tt', 'Tt', 'tt', 'tT', 'tt', 'tt', 'TT']
Recessive: [4, 4]
Dominant: [1, 2]
Mixed: [5, 4]
Generation: 2
Population: ['tt', 'TT', 'Tt', 'Tt', 'tT', 'Tt', 'Tt', 'tt', 'tT', 'TT']
Recessive: [4, 4, 2]
Dominant: [1, 2, 2]
Mixed: [5, 4, 6]
Generation: 3
Population: ['Tt', 'tt', 'TT', 'tt', 'tt', 'tT', 'TT', 'tt', 'tt', 'tt']
Recessive: [4, 4, 2, 6]
Dominant: [1, 2, 2, 2]
Mixed: [5, 4, 6, 2]
Generation: 4
Population: ['tt', 'tt', 'Tt', 'tt', 'tt', 'tt', 'tt', 'tT', 'tt', 'Tt']
Recessive: [4, 4, 2, 6, 7]
Dominant: [1, 2, 2, 2, 0]
Mixed: [5, 4, 6, 2, 3]
Just before returning from manyGenerations, call the
populationGraph function from the genetics library.
It expects three lists containing the recessive, dominant, and mixed
counts in that order. It will generate a graph like this when tested
on a population of size 10000, with probability of 0.5 for allele 'T',
and 200 generations:
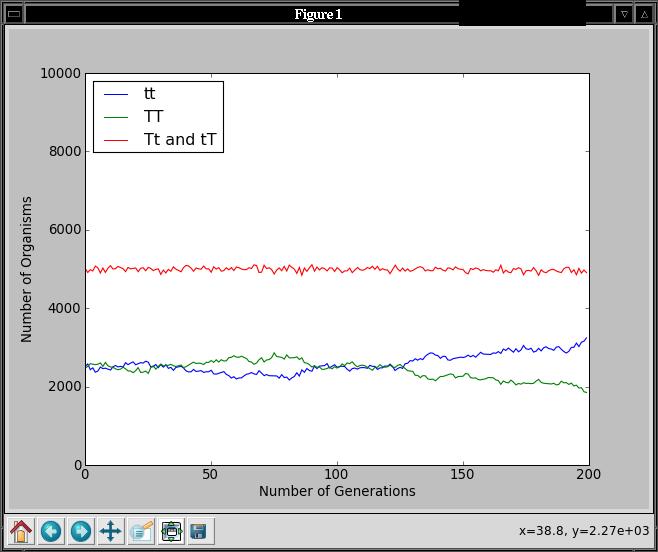
Regardless of the initial probability for the 'T' allele in the
initial population, you should see that the percentages of each
genotype remain fairly constant over time. This is predicted by the
Hardy-Weinberg
principle
These enhancements are not required and should only be attempted once all of the required elements described above are working correctly.
According to the Hardy-Weinberg principle, a population will remain in equilibrium only under certain conditions such as when mating is completely random. Let's explore how the proportion of genotypes in the population will change if we add preferential mating to our simulation.
Modify the main function so that it now asks the user whether or not to use preferential mating.
Modify the oneGeneration function so that it takes an additional parameter. This parameter will be a boolean representing whether preferential mating should occur. When it is False reproduction will work just as before. When it is True, tall organisms will prefer tall mates and short organisms will prefer short mates. Recall that if an organism has at least one 'T' allele it will be tall, otherwise it will be short.
You should implement preferential mating as follows. Randomly select two parents from the population. If they are both tall or both short, then immediately create a child. If they are different heights, then randomly re-select the second parent. Regardless of the new second parent's height, create a child.
Does the population remain in equilibrium once this feature is
added?
This lab was inspired by an assignment given at Harvey Mudd College
for a team-taught Biology and Computer Science course called
BioComp6 given by professors Zachary Dodds,
Ran Libeskind-Hadas, Eliot Bush, and Steve Adolph.
Once you are satisfied with your program, hand it in by typing handin21 in a terminal window.