CS21 Lab 10: Recursion
Run update21, if you haven't already, to create the
cs21/labs/10 directory.
Write a function that uses recursion to turn a string "inside-out". Your function should first pull out the middle character of the string, then the middle character from the remaining string, and so on and so forth, until there is only 1 or fewer characters left. The recursion also puts the pulled-out characters together, in the order they were pulled out. Here's a quick example, assuming the initial string is "CAT":
- pull out the middle letter: "A", so the remaining string is "CT"
- given the string "CT", pull out the middle letter. Since there is no true middle letter, use the one on the right (the "T")
- this leaves us with just the "C", so putting them all together gives "ATC"
Below are a few sample runs. Include a short main() function to ask the user for a string, and then send that string to your insideout(S) function. Your insideout(S) function should return the inside-out string back to main() for printing.
$ python insideout.py word: swarthmore! hmtorraew!s
$ python insideout.py word: ABCDEF DCEBFA
$ python insideout.py word: 12345 34251
In this last example, the initial middle character is the "3". After that is pulled out, the remaining string is "1245". Note the function as written chooses the "4", leaving the string "125". The middle character in that string is the "2", etc.
Extra Challenge
Are there any words that, after being turned "inside-out", are still
valid English words? If so, how many?
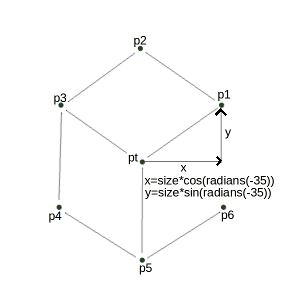
In a file called cubes.py, write a function called drawCube(pt,size,win) that draws what looks like a three-dimensional cube, given a corner point (pt), the size of the cube, and a graphics window (win) for the drawing. What your function should really do is draw three 4-sided Polygons, one for each side of the cube (see picture below). For example, the right side of the cube would be made of points pt, p1, p6, and p5.
Hints and requirements:
- use the clone() and move() methods to create the other points based on the given initial point (see diagram)
- note the math needed in the diagram below to calculate how far to move points p1 and p3 (if cloning pt)
- Use from math import * to import the sin(), cos(), and radians() functions
- make each side of the cube a different shade of one color (e.g., blue, dark blue, light blue), where the same side is always the same color (e.g., the left side is always the dark side)
- make sure everything scales, so your function works no matter what size and point are given
- include a simple main() function to test your drawCube() function
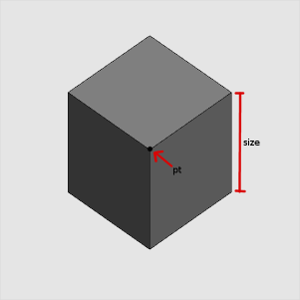
Now add a third function, recursiveCubes(pt,size,win), that uses recursion (and calls drawCube()) to draw the image below. Modify your main() function to call recursiveCubes(pt,size,win), instead of drawCube(pt,size,win).

Here's a fun function to compute:
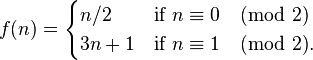
Known as part of the Collatz Conjecture, this function says, starting with any positive integer,
- If the number is even, divide it by two.
- If the number is odd, multiply it by 3 and add 1
This process is repeated over and over, using the result of one calculation as the starting point of the next, until we reach the number 1. Here's a quick example, using a starting number of 5:
- 5 is odd, so next number is 5*3 + 1 = 16
- 16 is even, so next number is 16/2 = 8
- 8 is even, so next number is 8/2 = 4
- 4 is even, so next number is 4/2 = 2
- 2 is even, so next number is 2/2 = 1, and we are done
Write a recursive function called collatz(n) that, given a positive integer, prints each number in the sequence, and returns how many steps were needed to reach 1. Include in your program a simple main() function that asks the user for the starting number, calls the recursive function, and prints the returned number of steps.
For example, if the user enters n=5, your program should display:
$ python collatz.py n: 5 5 16 8 4 2 1 num steps = 5 for n=5
Here are a few more examples:
$ python collatz.py n: 37 37 112 56 28 14 7 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1 num steps = 21 for n=37
$ python collatz.py n: 24 24 12 6 3 10 5 16 8 4 2 1 num steps = 10 for n=24
Extra Challenge
Use the following plotting function to display the number of steps needed vs n for all n from 1 to 10000, like this graph. In the function below, x and y are parallel lists (x contains all values of n, and y contains the number of steps needed for a given value of n).
import pylab
def plot(x,y):
pylab.plot(x, y, 'go')
pylab.grid(True)
pylab.xlabel('n')
pylab.ylabel('steps needed')
pylab.title('collatz plot: steps needed vs n')
pylab.show()
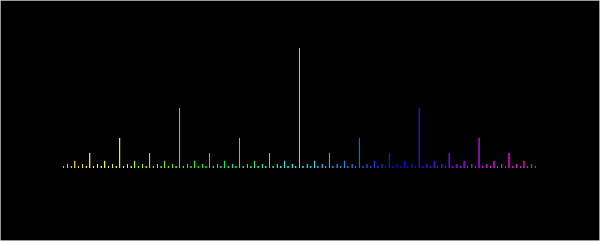
In a file called ruler.py, write a recursive function to display a set of lines like a ruler:
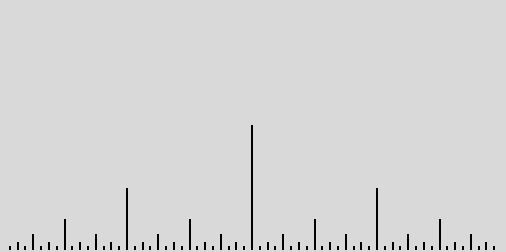
Your function should have only 3 parameters: the top point of the center line, the size of the center line, and a graphics window to draw the lines. Include a short main() function to test your recursive ruler function.
Extra Challenge
The image below uses the x-coordinate to determine the color of the line. This is more easily accomplished using a Hue-Saturation-Value (HSV) color model, where varying the hue corresponds to the common "rainbow" colors (ROYGBIV). Research an HSV to RGB transformation and use it (along with color_rgb(R,G,B)) to make a rainbow effect based on the x-coordinate.
Once you are satisfied with your program, hand it in by typing handin21 in a terminal window.