As always, run update21 to create this week's lab directory and copy over any starting-point files.

For this lab we will use the Zelle graphics library to solve several problems. First, you will write a program that allows a user to create a flag with random colors and a specified numbers of stripes and stars. Next you will use animation to create a Physics simulation of trajectories.

For this program, we want you to eventually create a flag with stars and stripes, like this:

To do this, however, we want you to make use of functions!

Write a program (called flag.py) that asks the user to enter the number of stripes, and then displays that many randomly-colored horizontal stripes. Note: your graphics window should always be the same size: 600x400. Only the number of stripes changes based on the user input.

drawStripes function

To accomplishy this you should define a function drawStripes(numStripes, window), which has two parameters: the number of stripes to display and the graphics window for drawing the stripes.

Here is an example:

$ python flag.py

number of stripes?: 13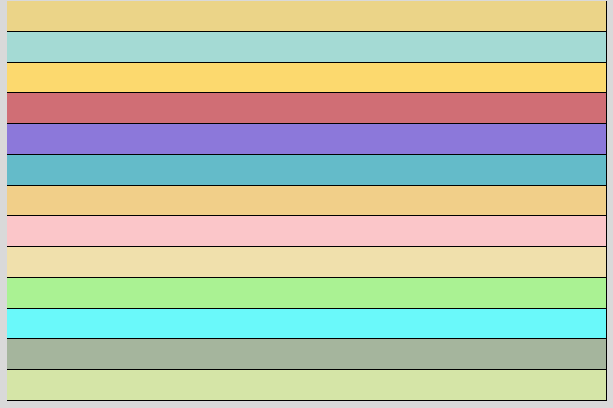

drawStar function

Now add a function, drawStar(centerPoint, size, color, window), to display a 5-pointed star.

This function should have 4 parameters:

• center point of the star
• size of the star
• color of the lines of the star
• window used to draw the star

Here is an example of the star:

And here is an example of the dimensions for a five-pointed star:

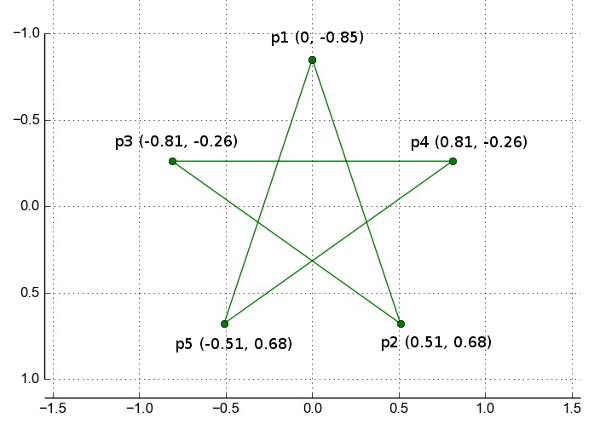
hints for drawing the star

• given the center point, you can clone it and move it to create each of the 5 points:

  p1 = centerPoint.clone() 
  p1.move(0,-0.85*size)
  

• given 5 points in a list, use the Polygon object to create the star. The Polygon constructor takes a list of point objects and will draw lines between them in the order given.
• note we can't "fill" the star with color (only the lines have color); if you really want filled stars, try making a 10-point star)

stars and stripes

Now modify flag.py to allow the user to create their own flag. Your program should ask the user for the number of stars and stripes, then display the randomly-colored stripes overlaid with a smaller, dark blue rectangle. Your program should then allow the user to click to place each star.

Here's an example (the user chose 21 stripes and 12 stars):

Using a technique called Euler's Method, we can get equations that approximate simple projectile motion (throwing a ball or firing a cannon). If you enjoy physics and math, here are the details: (a nice explanation from Amin Jazaeri at GMU).

Create a program called trajectory.py. For this program, you should display the motion of the ball, where the user specifies the angle of the throw. Assuming the following numbers:

          g = 9.8                            # gravity
          dt = 0.01                          # time step
          vx = 70*cos(angle-in-radians)      # velocity in x direction
          vy = -70*sin(angle-in-radians)     # initial velocity in negative y direction

you can then animate the motion of the ball as follows:

         start with the ball in lower left corner of the graphics window
         do the following 3 steps, as long as the ball hasn't "hit the ground":
             1. calculate how far to move the ball in the x and y directions:
                      dx = vx*dt
                      dy = vy*dt
             2. move the ball by dx,dy
             3. update vy due to gravity: vy = vy + g*dt

NOTE: to get the angle in radians, use the radians() function from the math library:

>>> from math import *
>>> radians(45)
0.7853981633974483
>>> radians(90)
1.5707963267948966

Here's an example of the animation:

Note: this program has lots of fun extentions, if you have time:

• add some kind of tracer (as shown in the video), so you can see the past trajectory even after the ball hits the ground
• add a randomly-placed target for the user to try to hit
• decide if the ball hit the target or not
• allow user to play again, keeping score of how many targets hit
• add Entry Objects to let the user enter the angle and the initial velocity (in the graphics window)

Once you are satisfied with each program, hand them in by typing handin21 at the unix prompt.