plot image
Imagine we are searching for some x in a list L. For example, we could have x=20 and L=[5,60,34,89,16,33]. Different search questions we can ask:
x in the list L? True/FalseFor now, let's just focus on the first question. Python gives us a simple way to answer that:
>>> x=20
>>> L=[5,60,34,89,16,33]
>>> print(x in L)
FalseIf we didn't have the in operator, we could easily write this as a function:
def search(x, L):
"""return True if x found in list L"""
for item in L:
if item == x:
return True
# only gets here if not found
return FalsePart of computer science is analyzing algorithms to see how good they are. Is the above search(x,L) function better, worse, or the same as just using x in L? Is there another way to search for x in L? How can we compare algorithms?
One simple way to compare algorithms is to just time how long they take on the same data. Another way is to examine the algorithm and figure out (roughly) how many steps it will take to execute. Furthermore, it is often useful to know how the number of steps needed depends on the size of the input data.
For example, in the above search(x,L) function, if len(L) is 10, then there are 10 comparisons done (if item == x). There are a few more steps in that function (e.g., returning True or False), but the for loop is the main part. If we double the size of the list L, we will double the number of steps needed. This is called a linear search, because there is a linear dependence between the size of the list and the number of steps needed (or the time it takes to run). If we were to plot the size of the list vs the number of steps needed, it would be a straight (linear) line.
If the data were sorted from low to high, is there a better way to search for x in L?
L = [5, 16, 33, 34, 60, 89]If we are still searching for x=20, there is no point searching past the 33, since we know the list is sorted from low to high, and we are already past what we are looking for.
Here is another example: if I say "I am thinking of a number from 1 to 100", and that when you guess, I will tell you if you are too high or too low, what is the first number you would guess?
A linear search would guess one number at a time, from 1 to 100.
A binary search would pick the middle and first guess 50. If that is too low, we can then concentrate on the upper half (51-100), and we have already eliminated half of the list! In a binary search, each guess should split the remaining list in half, and eliminate one half.
I want us to write two search functions: linearSearch(x,L) and binarySearch(x,L), which we can use in our other programs. For example, if we put these two functions in a file called searches.py, I want to be able to say from searches import * in my other programs and be able to use those two search functions!
Here is the start of searches.py, with the linearSearch(x,L) function in it. Note the test code at the bottom of the file:
def linearSearch(x,L):
"""return True if x is in L, False if not"""
for item in L:
if item == x:
return True
# only gets here if not found!
return False
if __name__ == "__main__":
# put test code here
L = range(10)
x = 5
print("%d %s %s" % (x, str(L), linearSearch(x,L)))
x = 500
print("%d %s %s" % (x, str(L), linearSearch(x,L)))The if __name__ == "__main__": part just decides if this searches.py file is being imported or run. If it is being run, like python searches.py, then we want to run the test code. If it is being imported, to be used in another program, then we do not want to run the test code (if we are importing it, we assume it already works!).
Here is an example of the binary search:
****** looking for g in:
['a', 'b', 'b', 'f', 'g', 'g', 'h', 'j', 'm', 'p', 'q', 'r', 'u', 'u', 'v', 'v']
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
L M H
Low: 0
High: 15
Mid: (low+high)/2 = 15/2 = 7
g < j, so high = mid - 1 = 6
['a', 'b', 'b', 'f', 'g', 'g', 'h', 'j', 'm', 'p', 'q', 'r', 'u', 'u', 'v', 'v']
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
L M H
Low: 0
High: 6
Mid: (low+high)/2 = 6/2 = 3
g > f, so low = mid + 1 = 4
['a', 'b', 'b', 'f', 'g', 'g', 'h', 'j', 'm', 'p', 'q', 'r', 'u', 'u', 'v', 'v']
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
L M H
Low: 4
High: 6
Mid: (low+high)/2 = 10/2 = 5
g found at index 5.And here is an example of what happens when the item we are looking for is NOT in the list:
****** looking for x in:
['c', 'e', 'g', 'i', 'k', 'k', 'l', 'o', 'o', 'r', 'r', 's', 's', 'z', 'z', 'z']
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
L M H
Low: 0
High: 15
Mid: (low+high)/2 = 15/2 = 7
x > o, so low = mid + 1 = 8
['c', 'e', 'g', 'i', 'k', 'k', 'l', 'o', 'o', 'r', 'r', 's', 's', 'z', 'z', 'z']
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
L M H
Low: 8
High: 15
Mid: (low+high)/2 = 23/2 = 11
x > s, so low = mid + 1 = 12
['c', 'e', 'g', 'i', 'k', 'k', 'l', 'o', 'o', 'r', 'r', 's', 's', 'z', 'z', 'z']
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
L M H
Low: 12
High: 15
Mid: (low+high)/2 = 27/2 = 13
x < z, so high = mid - 1 = 12
['c', 'e', 'g', 'i', 'k', 'k', 'l', 'o', 'o', 'r', 'r', 's', 's', 'z', 'z', 'z']
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
LMH
Low: 12
High: 12
Mid: (low+high)/2 = 24/2 = 12
x > s, so low = mid + 1 = 13
------ Low (13) > High (12) -------
x is not in the list.Notice that the algorithm continues until either the item is found, or the low and high indecies go past each other (low > high).
Here is the pseudo-code for binary search:
set low = lowest-possible index
set high = highest possible index
LOOP:
calculate middle index = (low + high)//2
if item is at middle index, we are done (found it! return True)
elif item is < middle item,
set high to middle index - 1
elif item is > middle item,
set low to middle index + 1
if low is greater than high, item not here (done, return False)Write the binarySearch(x, L) function in searches.py and add some test code to make sure it works.
assertThe assert statement is one way to add test code to your modules and libraries. Here is an example of adding assert statements to our searches.py file:
if __name__ == "__main__":
N = 100
L = range(N)
assert linearSearch(N/2, L) == True
assert binarySearch(N/2, L) == True
assert linearSearch(N*2, L) == False
assert binarySearch(N*2, L) == False
assert linearSearch(2, []) == False
assert binarySearch(2, []) == FalseWhen you run that, there will be no output if all tests pass. If one of the tests fails, you will see an AssertionError message.
One simple way to compare algorithms is to count how many steps each requires, or measure how long each takes to run on the same computer with the same data. In addition to this, it is often useful to know how the number of steps (or the runtime) will change as the size of the data increases. For instance, if we are searching for an item in a list, will the runtime double if we double the size of the list? If so, we call this a linear algorithm, since the time needed to search the list is directly proportional to the size of the list.
How many steps will linearSearch take, for a list with N items in it? How about binarySearch? Let's look at each and compare the algorithms.
For a linear search, we need to, at worst, check each item in the list. There's just a simple compare (if item == x) done for each item in the list. So, for the worst case, there will be N compares or N steps needed. If the item we are looking for is the first item in the list, then only 1 compare is needed, but that is the best possible case. A better measure would be the average case, requiring N/2 compares. Still, this clearly depends on the size of the list, N. So, if we double the size of the list, linear search will require, on average, or in the worst case, twice as many steps.
Since binary search splits the list in half each time, there are far fewer compares or steps. Given a list of size N=16, it is not hard to see there will at worst be 5 compares (just think about splitting 16 in half five times: 16-8-4-2-1). Mathematically, this can be computed with log-base-2 of N. If the size of the list is now doubled to N=32 items, there is only one additional step required! (log-base-2 of 32 is 6, log-base-2 of 64 is 7, etc).
In python, you can explore the base-2 logs with the following:
>>> from math import *
>>> log(16,2)
4.0
>>> log(32,2)
5.0
>>> log(64,2)
6.0
>>> log(1000000,2)
19.931568569324174
>>> log(2000000,2)
20.931568569324174So, for one-million items in a sorted python list, binary search will require at most, about 20 steps. If we double the size of the list to two-million, binary search now requires only about 21 steps. Notice how this is very different from the linear search! A linear search would require, at worst, two-million steps, compared to binary searches 21 steps.
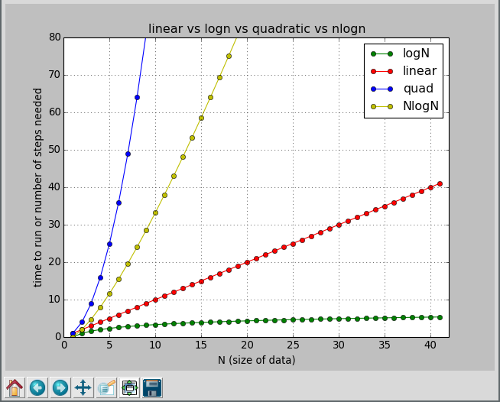
To summarize, we say linear search is an O(N) algorithm, and binary search is an O(logN) algorithm. The big-O notation just shows how each algorithm behaves versus the size of the data (N). Here are some other examples we will see in this class:
O(logN) one extra step, each time size of data doubles
O(N) number of steps doubles, each time size of data doubles
O(NlogN)
O(N*N) number of steps quadruples, each time size of data doublesAnd here is a simple plot of each, comparing the number of steps or runtime versus the size of the data:

plot image
How many steps for each of the following? And what happens to the number of steps when n doubles to 2n? Try to classify each of the following as one of these: O(logN), O(N), O(NlogN), O(N*N).
#############################################
# 1
n = int(input("n: "))
for i in range(n):
print i
#############################################
# 2
n = int(input("n: "))
for i in range(100):
print i*n
#############################################
# 3
n = int(input("n: "))
for i in range(n):
print i
for j in range(n):
print j
#############################################
# 4
n = int(input("n: "))
for i in range(n):
for j in range(n):
print i, j
#############################################
# 5
n = int(input("n: "))
for i in range(n):
for j in range(i,n):
print i, j
#############################################
# 6
n = int(input("n: "))
for i in range(n):
for j in range(10):
print i, j
#############################################
# 7
n = int(input("n: "))
while n > 1:
print n
n = n/2
#############################################
# 8
L = [1,2,5,7,13,21,24,25,26,33,34,38,50,57,58,63]
n = len(L)
mid = n/2
print L[mid]
#############################################
# 9
n = int(input("n: "))
for i in range(n):
k = n
while k > 1:
print i, k
k = k/2
#############################################searches.py fileWrite a program called lookup.py that simply asks for a word, and then tries to find the word in the system word list (/usr/share/dict/words). Here is an example:
$ python lookup.py
word: hello
Found
word: pickles
Found
word: sdkjflkdjf
NOT Found
word: In your program, include from searches import * to import our two search functions. If we are searching through the system word list, which is in alphabetical order, which search function should we use?
Another way to compare algorithms is by simply timing two algorithms on the same computer with the same data. For a spell-checking program, searching about 3000 times, through the system word list (99171 words), my linear search program took about 13 seconds to run, while the same program using binary search took only 4 seconds. What would happen to each if we doubled the size of the list we are searching through?
Here is an example of using the python time() function to see how long a block of code takes to run:
>>> from time import time
>>> t1 = time()
>>> x = 0
>>> for i in range(1000000):
... if i%2 == 0:
... x += 1
... else:
... x += 2
...
>>> t2 = time()
>>> total = t2 - t1
>>> print(total)
9.0005819798One of our students, Ben Schreiber, made a website to help students understand and learn various searching and sorting algorithms. His website includes a summary of binary search, an analysis of binary search, and a coding example with a song to help you remember the algorithm. If you are struggling to understand how binary search works (or the sorting algorithms we learn next week), check out Ben's musicAlgo.com site