WEEK10: recursion
---------------------------------------------------------------
M: recursive functions
recursion is when a function calls itself to get it's work done
recursion is most useful when the algorithm is one that repeats
something over and over, each time on a smaller set of the initial
data (ex: binary search)
MERGE SORT:
given a list...
if it has more than 1 item in it:
split it into to lists
sort each list
merge them back together
last week we wrote the merge(L1,L2,L3) function.
this week we are writing the mergeSort() function.
How should we do the "sort each list" step above?
IDEA: let's call mergeSort() to do that step!!!
So here it is...
def mergeSort(L):
n = len(L)
if n > 1:
half = n/2
L1 = L[0:half] # use slicing to split list into two
L2 = L[half:]
mergeSort(L1) # use another call to this function to
mergeSort(L2) # sort each sub-list!!
merge(L1,L2,L)
Think about the stack and how each called function is placed
on top of the stack. There is nothing wrong with a function
calling itself, as long as it doesn't repeat forever.
FACTORIAL EXAMPLE:
5! = 5*4*3*2*1
6! = 6*5*4*3*2*1 or 6*5!
7! = 7*6!
so n! = n * (n-1)!
math definition:
n! = 1 if n is 0, n*(n-1)! if n is greater than 0
**easy** to express this using recursion:
def factorial(n):
if n == 0:
return 1
else:
return n * factorial(n-1)
- try running /home/jk/inclass/factorialstack.py to see the stack
for the recursive factorial function:
$ python factorialstack.py
please enter a positive integer...
n: 4
-------------------------------
in factorial...stacknum = 1, n = 4
calling 4 * factorial(3)
in factorial...stacknum = 2, n = 3
calling 3 * factorial(2)
in factorial...stacknum = 3, n = 2
calling 2 * factorial(1)
in factorial...stacknum = 4, n = 1
calling 1 * factorial(0)
in factorial...stacknum = 5, n = 0
returning 1
returning 1
returning 2
returning 6
returning 24
factorial(n): 24
- try running a recursive program in the python tutor:
http://www.pythontutor.com
REVERSE A STRING:
- can you write a recursive function to reverse a string?
$ python revstr.py
string: we love computer science
reversed: ecneics retupmoc evol ew
Hint: if you have a string, s, and a working recursive revstr
function, what will revstr(s[1:]) + s[0] give you??
What is the base case/stop-the-recursion condition for this one??
def revstr(str):
""" Use recursion to reverse a given string. """
if len(str) <= 1:
return str
else:
return revstr(str[1:]) + str[0]
and just for fun, here is the non-recursive version:
def NRrevstr(str):
""" Non-Recursive version """
rs = ""
for i in range(len(str)-1, -1, -1):
rs = rs + str[i]
return rs
GRAPHICS:
- can you write a recursive function to draw concentric circles?
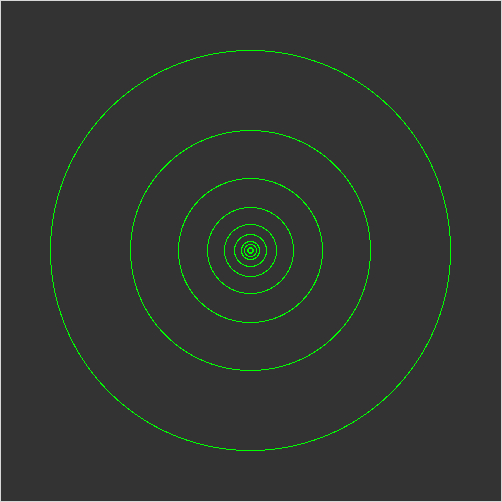 here's how it would be called from main:
reccircle(cenpt, size, color, win)
your function should draw a circle at the given center point,
with the given size and color, then call itself again with a
smaller size.
when should the recursion end?
def reccircle(p, radius, color, w):
""" draw recursive circles """
if radius > 1:
c = Circle(p, radius)
c.setOutline(color)
c.draw(w)
reccircle(p, radius*0.45, color, w)
here's how it would be called from main:
reccircle(cenpt, size, color, win)
your function should draw a circle at the given center point,
with the given size and color, then call itself again with a
smaller size.
when should the recursion end?
def reccircle(p, radius, color, w):
""" draw recursive circles """
if radius > 1:
c = Circle(p, radius)
c.setOutline(color)
c.draw(w)
reccircle(p, radius*0.45, color, w)
So far all of the recursive functions we have looked at could easily be written
without recursion. How about the following image? Can you think of ways to create
it with and without recursion?

 here's how it would be called from main:
reccircle(cenpt, size, color, win)
your function should draw a circle at the given center point,
with the given size and color, then call itself again with a
smaller size.
when should the recursion end?
def reccircle(p, radius, color, w):
""" draw recursive circles """
if radius > 1:
c = Circle(p, radius)
c.setOutline(color)
c.draw(w)
reccircle(p, radius*0.45, color, w)
here's how it would be called from main:
reccircle(cenpt, size, color, win)
your function should draw a circle at the given center point,
with the given size and color, then call itself again with a
smaller size.
when should the recursion end?
def reccircle(p, radius, color, w):
""" draw recursive circles """
if radius > 1:
c = Circle(p, radius)
c.setOutline(color)
c.draw(w)
reccircle(p, radius*0.45, color, w)
