Week 12¶
Big-O Notation¶
Used for analysis of algorithms. Gives an approximation of the number of steps.
Definition of Big-O:
f(x) is O(g(x)) as x goes to infinity if and only if there exists positive constants m and x0 such that
f(x) < mg(x) for all x >= x0
Example 1:
- f(x) takes 5 steps
- g(x) = 1
- f(x) <= mg(x) for all m >= 5
Therefore, f(x) is O(1).
Example 2:
- An algorithm takes 3n + 6 steps
- We think that it is O(n)
- f(x) <= mg(x) for all m >= 4 and x0 >= 6
Example 3:
- Algorithm: 2n2 + 3n + 6
- We think that this is n2
- f(x) <= mg(x) for all m* >= 3 and x0 >= 5
Main classes of orders:
- constant: O(1)
- Logarithmic: O(log n)
- Linear: O(n)
- Superlinear: O(n log n)
- Polynominal: O(nm)
- Exponential: O(mn)
Lists¶
Definition: an ordered collection of items.
Python has an implementation of lists. How do they work and how are they implemented?
First of all: What operations can we do with a list?
- get the length (
len(ls)) - index into (
ls[3]) - add to end (
ls.append("pony")) - add to middle (
ls.insert(3, "a")) - remove from end (
ls.pop())
Implementation of Lists in Computer Memory¶
Lists are implemented in two main ways:
Stored in consecutive locations
1000 1001 1002 1003 1004 1005 1006 1007 1008 1009 1010
'a' 'b' 'c'A list like this has three pieces of information:
- Base address
- Block size (size of each item)
- Capacity (maximum number of items)
- Length (number of items)
How long does it take us to do the operations?
- Get the length (constant time)
- Index into the list (constant time -- just take base address, index, block size, and calculate)
- Insert at end (constant time -- UNLESS the list is already full)
If the list is already full when we want to insert at the end, we need to allocate a new chunk of memory to act as the new list, and copy everything over. That will take linear time.
- Insert in middle (linear time -- copy everything over by one)
Linked Memory
Linked memory does not require that the items are stored in one contiguous block. Rather, items are stored as a chain of nodes, where each node contains two pieces of information: The value of the item it is storing, and a pointer that links to the next node.
| Linked List -- Visualization | Linked List -- what actually happens in memory |
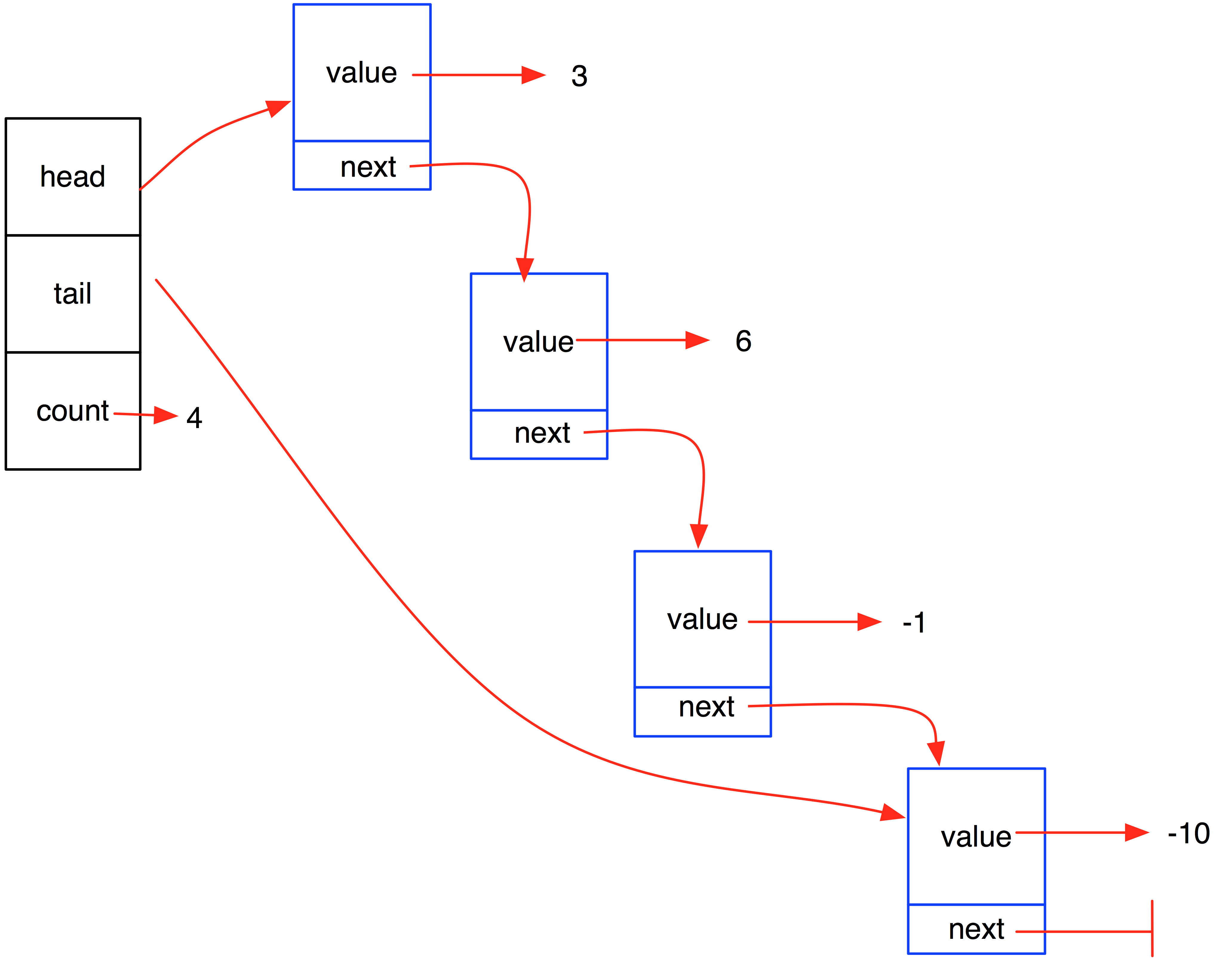
|
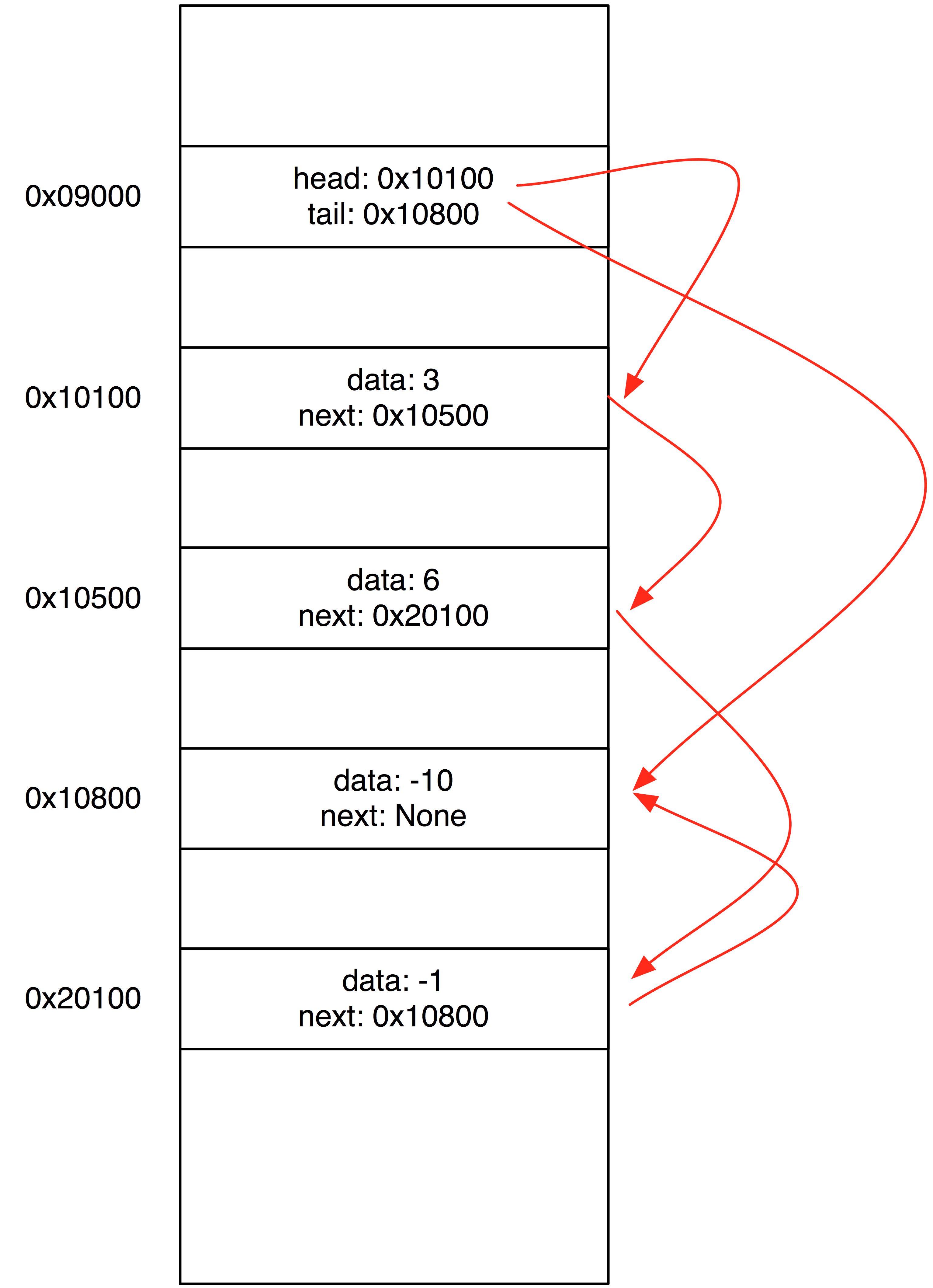
|
Operations:
- Get length (constant)
- Index into (linear)
- Insert at (linear, but does not require copying)
- Delete from (linear, but does not require copying)
- Insert at end (constant)
Linked lists have some advantages over consecutively-stored lists:
- Do not require a contiguous chunk of memory
- Insertion and deletion from the ends take constant time
The second point makes linked lists ideal for certain applications, such as queues and stacks.
Implementing Linked Lists¶
All linked lists have two classes:
The Node class describe the objects that store the data. Each Node also has a pointer to the next Node in the chain.
(A pointer is just a memory address -- we can find the next Node in the chain using its address.)
class Node(object):
def __init__(self, data):
self.data = data
self.next = None
def getData(self):
return self.data
def getNext(self):
return self.next
def setData(self, data):
self.data = data
def setNext(self, next_node):
self.next = next_node
A LinkedList object keeps track of the head (the first Node in the chain) and the tail (the last Node in the chain):
class LinkedList(object):
def __init__(self):
self.head = None
self.tail = None
One of the things that we often need to do with a LinkedList is to traverse it -- i.e. go through the entire chain from beginning to end, and print out each of the items in turn:
# This is for LinkedList
def __str__(self):
output = ""
current = self.head
if current == None: # empty linked list
return "<None>"
while(current != None):
output += str(current)
current = current.getNext()
return output
This means that we need to add an __str__() method for Node:
# This is for Node
def __str__(self):
output = str(self.data)
if self.next == None:
output += " --| "
else:
output += " --> "
return output
# Complete Node class
class Node(object):
def __init__(self, data):
self.data = data
self.next = None
def getData(self):
return self.data
def getNext(self):
return self.next
def setData(self, data):
self.data = data
def setNext(self, next_node):
self.next = next_node
def __str__(self):
output = str(self.data)
if self.next == None:
output += " --| "
else:
output += " --> "
return output
# Complete LinkedList class
class LinkedList(object):
def __init__(self):
self.head = None
self.tail = None
def __str__(self):
output = ""
current = self.head
if current == None: # empty linked list
return "<None>"
while(current != None):
output += str(current)
current = current.getNext()
return output
node1 = Node(3)
node2 = Node(5)
node3 = Node(-1)
node4 = Node(-6)
node1.setNext(node2)
node2.setNext(node3)
node3.setNext(node4)
linkedlist = LinkedList()
linkedlist.head = node1
linkedlist.tail = node4
print linkedlist