Run update35 to copy some useful files to your cs35/labs/03 directory. You will not turn in any code this week, and will instead turn in written solutions to the box outside Charlie's office, SCI 255. Note that although your solutions are written and not electronically submitted, the deadline is still Wednesday night at 11:59 p.m. and late work will not be accepted.

You may work with a partner this week. However, you should work together on each problem and are both responsible for fully understanding all problems you hand in. Make sure that both names are on the pages that you hand in.

1. C-4.20 An array A contains n-1 unique integers in the range 0 to n-1. Thus exactly one number in this range is missing in the array. Design an O(n) time algorithm for determining this missing number, using at most O(1) extra space. (In other words, you cannot make an extra array of size n, but you can store a constant number of extra variables.)
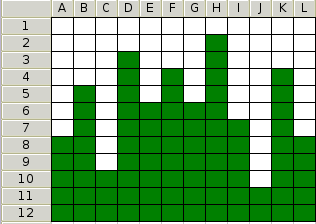
2. Based on C-4.26 The image below shows an n by n grid that is stored in memory as a two dimensional array. The element at row i column j can be indexed in constant time using grid[i][j]. Each cell in the grid contains either a 1 or a 0 (indicated in the figure with green and white blocks). In any column, all the one's appear before any of the zeros. Given such a grid, design an O(n) algorithm for finding the column with the most ones (tallest green tower). Note there are O(n^2) cells, so you cannot check every cell in the grid.
3. Suppose I want to find the Big-O runtime of a certain algorithm, but I do not have access to the description of the algorithm. All I know is that the runtime of the algorithm is given by the following recursive definition: T(n)=T(n-1)+O(n), meaning the time it takes to process an input of size n is equivalent to the time it takes to process an input of size n-1 plus O(n) more time. Assume T(0) is a constant. We could write T(1) <= T(0)+c*1 and T(2) <= T(1)+c*2 <= T(0)+c(1+2). Determine a Big-O bound on the runtime of T(n) and prove your result using induction.
4. Describe an algorithm for finding both the minimum and maximum of n numbers using fewer than 3n/2 comparisons. The following pseudocode finds the max using n-1 comparisons.

   findMax(Array A, size n>0):
     max=A[0]
     for i in 1 to n   (inclusive)
       if(A[i] > max)
         max=A[i]
     return max
   

5. Give the best Big-O bounds on the runtime of the following functions. By "best" Big-O bounds we mean the bounds that most-closely describe the actual run time of the function. E.g., for a linear algorithm the best Big-O bound is O(n), not O(n^2), even though linear algorithms are O(n^2) as well.

   Ex1(n)
    for(i=0; i<n; i++)
      a = i
   
   Ex2(n)
    for(i=0; i<n; i+=2)
      a = i
   
   Ex3(n)
    for(i=0; i<n*n; i++)
      a = i
   
   Ex4(n)
    for(i=0; i<n; i++)
      for(j=0; j<=i; j++)
        a = i
   
   Ex5(n)
    for(i=0; i<n*n; i++)
      for(j=0; j<=i; j++)
        a = i
   
   Ex6(n)
    k=1
    for(i=0; i<n; i++)
      for(j=0; j<k; j++)
        a = j
      k=k*2
   

Perform an experimental analysis that compares the relative running times of the functions you considered in Ex1 through Ex6 above.

To run these experiments you will need to use different sizes of n, depending on the example being tested. For fast algorithms you will need to use very large n, starting with 100000 or 1 million. Slower algorithms might require you to test with n as small as 10 or 100. When you implement the functions above, we recommend that you use long integers instead of ints. Like the long integers in Python, longs in C++ can store larger numbers than ints. (Unlike the long integers in Python, long integers in C++ are limited and can not be arbitrarily large.)

After you run update35 your cs35/labs/03 directory will contain some helpful files:

• timer.h and timer.cc: Defines a Timer class that works like a stop watch. With a Timer t t.start() will start the timer and t.stop() will stop the timer, allowing you to get the recorded time with t.getRecordedTime().
• timerTest.cc demonstrates the use of the Timer to measure the performance of an example function. The basic idea is, for each input size you want to measure:
  1. Start the timer.
  2. Run the function you want to measure the performance of on a single input size.
  3. Stop the timer.
  4. Print the input size and recorded time.
  timerTest.cc also demonstrates some new C++ output formatting options and how to use long integers in your example functions.
• ex4results.txt: A sample data file that can be used as input to the pgraph program, which allows you to view your results graphically. To see a graph of these example results, run:

    $ pgraph ex4results.txt
  

  in your terminal window.

  When you create your own data files, please put your name(s) in the graph title and label your data with appropriate names. When you run pgraph you can save your results as a Postscript (.ps) file: click the save icon (the floppy disk, on the bottom right), type a filename (such as ex4results.ps), and select "Postscript (*.ps)" as the file type. You can then print your results from your terminal window using the lpr command. For example:

    $ lpr ex4results.ps
  

Hand in your work to the box outside Charlie's office by 11:59 p.m. Wednesday night. Do not turn in any work with handin35.