This study guide includes topics covered since Quiz 3; you should also study all concepts from earlier in the course. The earlier study guides are available here: Quiz 1, Quiz 2, Quiz 3 .

You should be able to define or explain the following terms:

• The Dictionary abstract data type
• Generalized indexing (i.e., associative arrays)
• Collisions, mapping and compression
• Hash tables, hash functions, hash code, a hash table's load factor
• Importance of hash functions, load factors, capacity, etc in performance
• Separate chaining and linear probing (as well as possible extensions)
• Tradeoffs between BST and HashTable dictionary representations
• Various strategies for handling keys (e.g., allowing duplicates in priority queues vs unique keys in BST and Dictionaries)
• graph, vertex, edge
• directed, undirected graphs
• weighted, unweighted graphs
• adjacent, neighbor, outgoing edges, incoming edges, out-degree, in-degree, degree
• path, reachable, path length, distance, cost
• connected component, strongly-connected component
• adjacency-list representation, adjacency-matrix representation
• breadth-first search, depth-first search of a graph
• recursive depth-first search
• shortest path problem
• Dijkstra's algorithm
• cycle
• directed acyclic graph (DAG)
• topological sort
• trees
• spanning tree, minimum spanning tree (MST)
• Prim's algorithm for discovering an MST
• Kruskal's algorithm for discovering an MST (at a high level)

Practice problems

1. Using chaining to resolve hash collisions, insert the following five items into a hash table of capacity 5, in the order given (from top to bottom):

   Key	Hash code
   A	1
   B	1
   C	1
   D	0
   E	2



2. Repeat using linear probing to resolve hash collisions, instead of chaining.


3. Consider the following hash function, like the function in hashTable-inl.h:

     int hash(int key, int capacity) {
       return key % capacity;
     }
   

   1. Complete the following code so that the total running time is asymptotically proportional to n^2:

        void f(int n) {
          HashTable<int,string> ht(n);  // Creates hash table with capacity n.
          for (int i = 0; i < n; ++i) {
      
            ht.insert(________________, "skittles");
          }
        }
      

   2. Complete the above code so that the total running time is asymptotically proportional to n.
   (In either case, assume that the hash table does not resize.)


4. Consider the following graph:
   
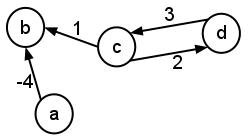
   1. Give the adjacency-list representation of the graph.
   2. Give an adjacency-matrix representation of the graph.


5. Play Charlie Garrod's Dijkstra Adventure Game by running dag in a terminal window. Be sure to play once or twice with the --random option:

     $ dag --random
   

   (I'm sorry for how tedious the game can be -- the graph is big!)



6. Consider the following set of courses and their prerequisites:
   • PHYS 005: none
   • PHYS 007: PHYS 005 and MATH 025
   • PHYS 008: PHYS 007 and MATH 033
   • PHYS 014: PHYS 008, MATH 027, and MATH 033
   • PHYS 050: MATH 027 and MATH 033
   • PHYS 111: PHYS 014 and MATH 033
   • PHYS 112: PHYS 014, PHYS 050, and MATH 033
   • PHYS 113: PHYS 111 and MATH 027
   • PHYS 114: PHYS 111 and MATH 033
   • MATH 025: none
   • MATH 027: none
   • MATH 033: MATH 025
   Assuming that a physics student can take only one course at a time, use a graph algorithm from this course to find a sequence of courses that satisfies the prerequisites. Show the graph on which you executed the graph algorithm.


7. In lecture we saw a variant of recursive depth-first search. Recursive depth-first search is extremely simple and elegant if the algorithm does not need to track additional information or return any value:

     dfs(G, src):                           // This function initializes the
         isVisited = new dictionary         // dictionary and calls the
         for each vertex v in G:            // recursive helper function.
             isVisited[v] = false
         recursiveDfs(G, src, isVisited)
   
     recursiveDfs(G, src, isVisited):       // This recursive function
         isVisited[src] = true              // searches the graph.
         for each neighbor v of src:
             if !isVisited[v]:
                 recursiveDfs(G, v, isVisited)
     

   1. Execute dfs on the following graph, using s as the source vertex. Draw the stack frame diagram for the program as it executes. (Assume that isVisited refers to a single copy of the dictionary for all frames of the stack.)
      
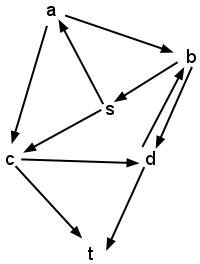
   2. Modify the pseudocode above to accept a second vertex, dest, as an argument. Return true if there is a path from src->dest in G, and return false otherwise.
   3. Modify the pseudocode again to return the length of some src->dest path (not necessarily the shortest path) if there is a path from src to dest in G. If there is no src->dest path, return -1.
   4. Write a version of breadth first search and depth first search that determines if a graph is connected.
   5. Write a version of depth first search that returns all vertices in the same component as some source vertex.


8. Compare the run time of all key Graph methods using an adjacency list versus adjacency matrix representation. Express each in terms of the number of vertices (n) and edges (m) in the graph.
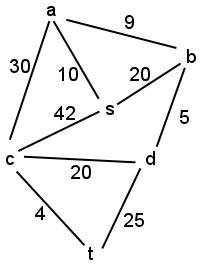
9. Execute Prim's algorithm to find a MST of the following graph using s as the initial vertex. For each step of the algorithm, show which edges and vertices have been selected for the MST up to that step.


10. What is the run time of breadth first search? depth first search? Dijkstra's? What about for a topological sort? How does the run time change if we use a stack, queue, or priority queue for the topological sort algorithm?

Home Page