CS56 Computer Animation: Lab 2

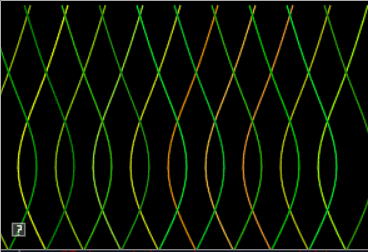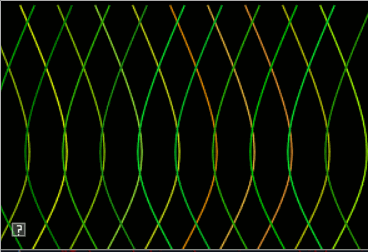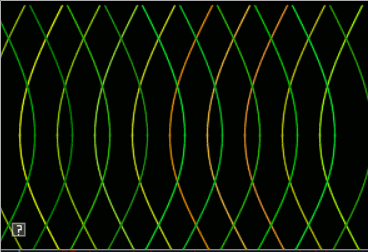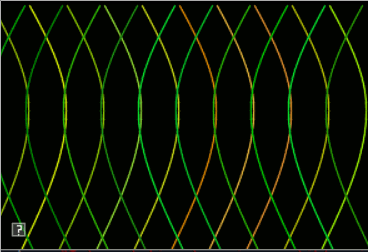
The goals of this lab are to implement

• animations using linear interpolations
• animations using cubic interpolations

Get the source

The interpolation assignment has been added to your AnimationFramework repository. To get the source, run

> cd cs56/AnimationToolkit 
> git pull
> cd build
> cmake ..; make

You should now have a new directory under assignments called a2-interpolation.

Assignment 2: Howl's moving casteljau

Due September 20

In this assignment, you will interpolate between points using linear interpolation. \[ p(t) = (1-t) p_0 + t p_1 \]

And cubic interpolation with Bezier curves \[ p(t) = (1-t)^3 b_0 + 3t(1-t)^2 b_1 + 3t^2(1-t) b_2 + t^3 b_3 \]

Question 1: Gradient (5 points)

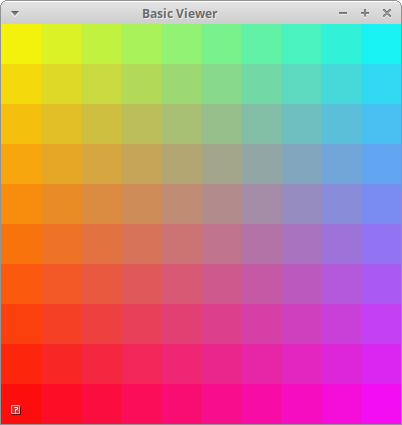
A color gradient uses linear interpolation to gradually change from one color to another based on position. In class, we computed a gradient in the demo colorLerp2.cpp

For this question, modify the code in gradient.cpp to implement a 2D gradient. Your program should open a square window and draw NxN cubes to fill it. The color of each cube will be a function of four colors and the cube's position. The four colors will correspond to the four corners of the screen: NE, SE, SW, NW.

To run your program from the build directory, type

build> ../bin/a2-gradient 

Let's suppose that

• The northwest corner has color yellow (1,1,0). Let's name this color $C^{nw}$.
• The northeast corner has color cyan (0,1,1). Let's name this color $C^{ne}$.
• The southwest corner has color red (1,0,0). Let's name this color $C^{sw}$
• The southeast corner has color fuchsia (1,0,1). Let's name this color $C^{se}$.

A 2D gradient is computed in two steps. Suppose our cube is at position $(p_x, p_y)^T$. First, we interpolate from west to east. Let $t^x \in [0,1]$ be computed based on $p_x$ and the window's width.

\( C_0^x = C^{nw} * (1-t^x) + C^{ne} * t^x \\ C_1^x = C^{sw} * (1-t^x) + C^{se} * t^x \)

Second, interpolate $C_0^x$ and $C_1^x$ based on the y direction. Let $t^y \in [0,1]$ be computed based on $p_y$ and the window's height.

\( C = C_0^{x} * (1-t^y) + C_1^{x} * t^y \)

The final result is below

Question 2: Degree-2 Bezier Curve (10 points)

In class, we derived the Bezier curve for cubic interpolation. For this question, derive the Bezier curve for a degree-2 polynomial.

1. (5 points) In class, we saw that the formula for a nth-degree Bezier curve is \[ p(t) = \sum_{i=0}^n B_i^n(t) b_i \] What is the polynomial for a degree-2 Bezier curve? How many control points does it have?
2. (5 points) How can we use de Casteljau's algorithm to interpolate using a degree-2 Bezier curve?

Please include your answers as part of your README for this week.

Question 3: Classy Cubic (10 points)

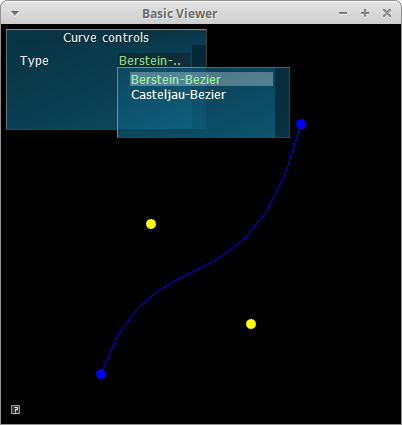
For this question, you will implement classes for cubic curves computed using either Bernstein polynomials or De Casteljau's algorithm.

You have been given skeleton code in Cubic.h and Cubic.cpp. These files implement a base class, Cubic, with two subclasses: CubicDeCasteljau and CubicBernstein. The base class has setters and getters for the control points. The base class also defines two methods. The draw() method should draw the curve using ADrawLine (defined in libsrc/ui/AGLObjects.h). The interpolate(double) method should return the value of the curve at the given time. The implementation for interpolate is in the subclasses. CubicDeCasteljau should implement interpolate using de Casteljau's algorithm. CubicBernstein should implement interpolate using Bernstein polynomials.

Once your class is complete, you can test both your implementations using the application defined in drawCubic.cpp

To run your program from the build directory, type

build> ../bin/a2-drawCubic 

Question 4: Animating position (5 points)

For this question, we will re-use the class you made in Question 3 to update the position of a particle. Implement your solution in the file particleCubic.cpp. The algorithm for animating position is the same as the particleLerp.cpp example from class. However, instead of linear interpolation, we use cubic interpolation. Your solution should draw the curve as well as the particle.

To run your program from the build directory, type

build> ../bin/a2-particleCubic 

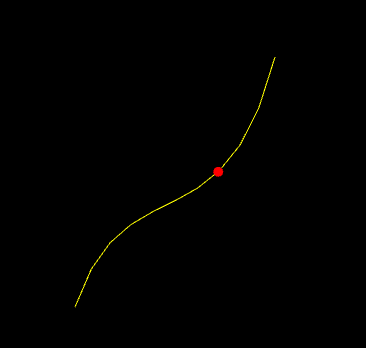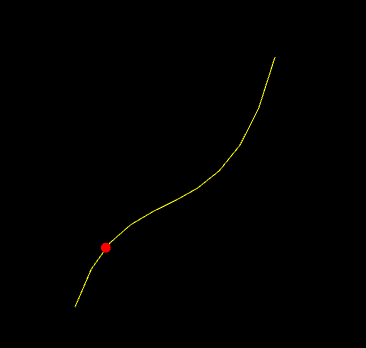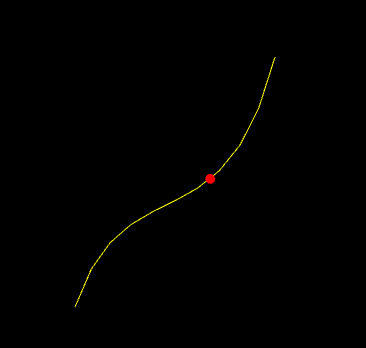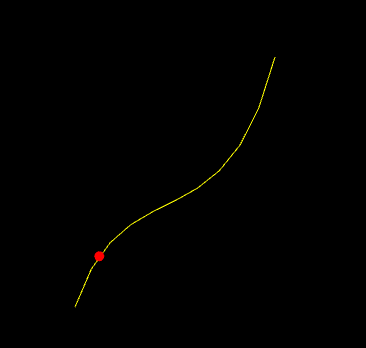
Requirements:

• The particle should take 5 seconds to travel the curve.
• The particle should wrap to the beginning of the curve when it gets to the end. You can use any algorithm you want for this, but the simplest solution involves using the elapsed time and fmod.

Question 5: Animating curves (5 points)

For this question, we will re-use the class you made in Question 3 to linearly interpolate between two curves. Implement your solution in the file animateCubic.cpp.

To interpolate between two curves, we only need to interpolate each of the control points. Your basecode defines two curves: curve1 and curve2. To interpolate back and forth between them you need to let the t vary from 0 to 1 and then from 1 to 0.

To run your program from the build directory, type

build> ../bin/a2-animateCubic 

Requirements:

• The interpolated curve should ping pong between curve 1 and curve 2.
• You should also interpolate the color.

Question 6: Screensaver (15 points)

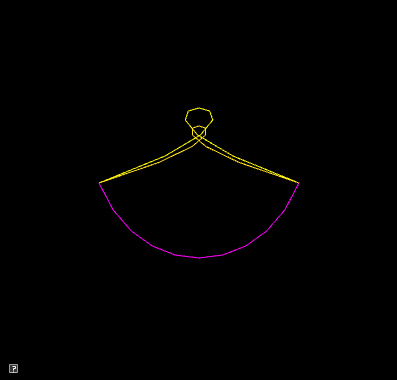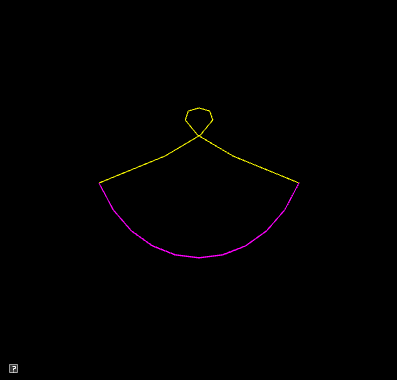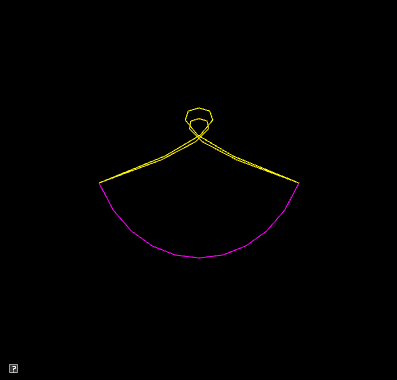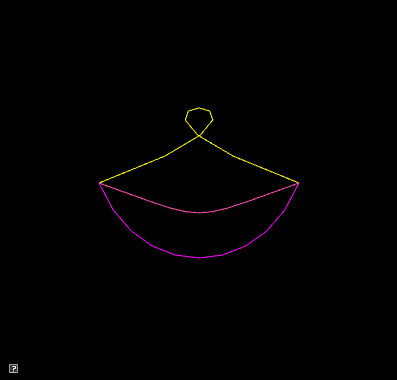
In the previous question, we oscillated between two curves. In this question, we will interpolate between a series of curves. This question has two parts.

To run your program from the build directory, type

build> ../bin/a2-screensaver 

Part 1: Animate a single curve (10 points)

We will interpolate between curves having random control points. You will need three curves.

• the starting curve (e.g. curve1 from before),
• the ending curve (e.g. curve2), and
• a curve that stores the current interpolation between them. Let's call this curve 'current'

When the current curve reaches curve 2, we compute a new curve to interpolate towards. The algorithm looks like

if t > 1
   t = 0
   curve1 = current
   curve2 = new random curve

current = interpolate between curve1 and curve2 based on t

Requirements:

• You should randomize colors
• The animation should run forever (don't hardcode the number of curves)
• All control points should be within the bounds of the window
• Draw curve1, curve2, and current
• Implement your animation in update(), not draw()

Part 2: Implement a trail effect (5 points)

To implement a trailing effect, we save previously interpolated curves in a list. So we don't run out of memory, we store at most N previous curves. In the demo below, N is 50.

In the simplest trail implementation, we would add a new curve to our list every frame. In other words, whenever we update the current curve, we would also add it to our list. However, this creates a trail that has the lines close together. You should try this first.

To make a prettier effect, we should only save the current curve only after T seconds have passed. In the demo below, X is 0.1 seconds. The algorithm looks like

if timer > T
   timer = 0
   add current curve to a list
   if trail size > max size
      remove oldest curve from list

Requirements:

• You should randomize colors
• The animation should run forever (don't hardcode the number of curves)
• All control points should be within the bounds of the window
• Space out saving the current curve by T seconds. T > 0
• Store at most N curves in your trail. N > 5
• Implement your animation in update(), not draw()
• Implement your animation in update(), not draw()

Extra Credit (Up to 3 points)

Option 1: Derive and implement a degree-N curve

Option 2: Implement a cool scene using curves

• Play with colors (gradients, palettes, jitter). Use a cubic curve to animate color.
• Use sine/cosine to animate the control points
• Let the user specify control points with mouse click
• Animate the positions, colors, and scale of different shapes using cubic curves

Submission Requirements (1 points)