The goals of this lab are to give you experience implementing nontrivial algorithms and to give you practice with asymptotic analysis and formal proofs. Concepts you will be familiar with after this lab include:

• sorting
• big-O notation
• formal proofs
• runtime analysis
• unit test

For this assignment, you will be working with a partner. Both partners should be present and working on the code together. You will both be responsible for understanding all concepts, so dividing and conquering is not an option. The academic integrity policy applies to the entire pair; you cannot work or share code with anyone outside your partner.

You and your lab partner will share the same git repository, which is named lab03-<user1>-<user2>.git Please access your lab by cloning the appropriate git repository, e.g.:

$ git clone git@github.swarthmore.edu:CS35-s17/lab03-adanner1-jbrody1.git

This lab consists of three parts:

• Proving the asymptotic i.e. big-O complexity of two functions.
• Analyzing and empirically testing code to understand complexity.
• Implementing and testing a quickSort implementation.

As with Lab 02, you and your partner will share a git repository. Please remember that, as with all partnered labs, both partners must learn this material. Do not divide up this lab to give one team member the theory material and another member the sorting algorithm.

Use the formal definition of Big-O notation to prove the following statements:

1. $n^2 +3n + 18$ is $O(n^2)$
2. $2n^3 - 19$ is $O(n^3)$

In order to complete this assignment, you will need to produce a document containing some mathematical expressions and figures. You will commit and push this document to your GitHub repository; the document may take the following forms:

• A PDF file named WrittenLab.pdf containing formatted text
• A LaTeX file named WrittenLab.tex containing formatted text

Your team must submit the document electronically by adding it to your git repository. In particular, you are not allowed to submit in one of the following forms:

• A raw text document (regardless of formatting)
• A scan of a written document (even if the scanned document is a PDF)
• A Microsoft Word file or similar word processor document (although you may write the homework in that format and then export a PDF from it)
• A piece of paper turned in by hand

Using LaTeX

LaTeX (pronounced lah-tek or lay-tek) is a document preparation system frequently used to produce conference papers, dissertations, and other academic works (in addition to other material). With LaTeX, you code your document much as you would an HTML document or a Python program. For instance, the LaTeX code

I'm \textit{not} making this up: $e^{i\pi}=-1$

produces

$\text{I'm } \textit{not} \text{ making this up: } e^{i\pi} = -1\ .$

You are not required to learn LaTeX for this course. However, it may be easier to use basic LaTeX to complete your homework than to use something like Microsoft Word's equation editor. In case you're interested, the following files are already part of your repository:

• LearningLaTeX.tex: A LaTeX document with some examples of how to use LaTeX to write the things you need to write in this lab. You should look at the .tex file before looking at the .pdf it produces.
• WrittenLab.tex: A LaTeX document containing your homework problems and places for you to fill them in. This also includes places to include your mystery function writeup from part 2.

In this part of the lab, you will first analyze six simple loop structures and determine their asymptotic runtime complexity in terms of big-O notation. Then, using the provided program function_timer, you will graph the empirical runtimes of the functions.

The Functions

Begin by identifying the Big-O runtime for each of the following functions. Provide a brief justification for each answer---full proofs are not necessary. Give the strictest comparison you can find; e.g., don't give $O(2^n)$ if the function is also $O(n)$, and leave out any second-order terms: give $O(n^2)$ instead of $O(n^2 + n))$.

    
Ex1(n):
  for i=0...n
    a = i

Ex2(n): 
  for i=0...2*n
    a=i;

Ex3(n) 
  for i=0...n
    for j=0...i
      a=i;

Ex4(n):
  for i=0...n*n
    a=i

Ex5(n):
  for i=0...n
    for j=0...i*i
      a = i

Ex6(n):
  k=1
  for i=0...n
    for j = 0...k
      a = i
    k = 2*k

Hint: Analyze double-for-loops as we did in class. If the analysis is still hard to figure out, try to count the number of inner loop iterations for both small and large values. For example, for Ex3, the number of inner loop iterations when $i=0,1,2$ is $1,2,3$. When $i=n-2,n-1,n$ the number of inner loop iterations is $n-1, n, n+1$. Then, try to identify a pattern.

Using function_timer to Inspect the Functions

Each of the above functions has been implemented and packaged into a single executable function_timer that we provided for you in your git repository. However, to make things interesting, we scrambled the order of the functions. Your job will be to match each function with its corresponding name. The function_timer program will provide empirical runtime data for each of the above functions, in a form that can be graphed by another tool called gnuplot.

To use this program, you must pick the following:

• Which function(s) to plot. For each function, you must provide a command-line argument of the form -1, -2, etc.
• The minimum and maximum values for n. Remember, for slow algorithms n should be small, or the program will take a long time. For fast functions, you'll need to give a very large value for n, or you won't be able to see anything meaningful on the plot. Start with small n for each plot and work your way up.

For instance, you can graph functions 5 and 6 within the range 10<=n<=100 by running this command:

$ ./function_timer -5 -6 -n 10 -m 100 | gnuplot

If this command does not work the first time, you may need to change the permissions of the function_timer file once before running it.

chmod 700 ./function_timer

Then run the first command again.

This will produce the following graph:

To save a graph as a png file, add a -s <name of file>

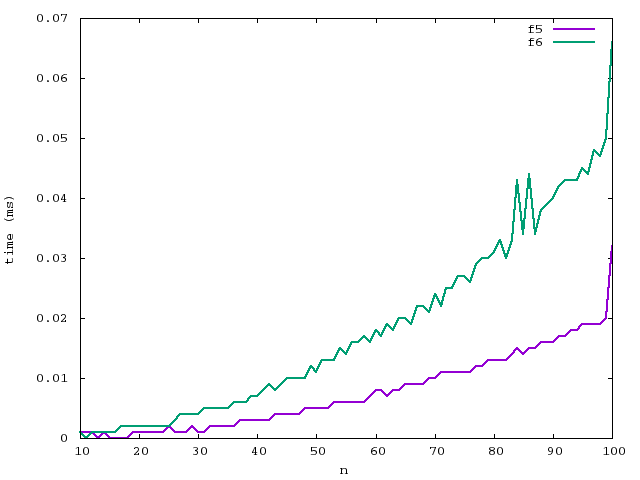
$ ./function_timer -5 -6 -n 10 -m 100 -s 56.png | gnuplot

Your writeup should include at least two graphs justifying your answer. Instructions for how to include images in a .tex file are in WrittenLab.tex.

For the coding part of this lab, you will implement the quickSort sorting algorithm we saw in class. Your starting repository includes the following files:

• quickSort.h, quickSort.cpp: this is where you will write your quicksort code.
• main.cpp: A small program that uses your sorting algorithm, taking an input array from standard input.
• tests.cpp: A file where you will write your unit tests.
• Makefile: The file make uses to understand how to compile your code.

As always, files that you'll need to change are marked in blue. However, you'll be responsible for understanding all of the code.

To complete this lab, you should implement the quickSort function in quickSort.cpp, as we discussed in class. You'll need to be careful to follow the algorithm closely and to manipulate array indices accurately. Expect to have bugs in your first attempt. That's OK. Understanding what your bugs are and how to go about debugging/fixing them is a big part of becoming an excellent coder!

Unit Tests

To assist in the debugging process for this (and future!) labs, we're introducing a debugging tool called unit tests. A unit test is a small C++ function that tests a small piece or aspect of your code. Test Driven Development is a software engineering practice that uses extensive unit tests to ensure that software acts as expected. In principle, it makes code more reliable and makes bugs easier to identify and isolate.

We'll be using a unit testing framework called UnitTest++. This will let us easily write short effective unit tests for labs this semester. Write your unit tests in tests.cpp. We've given you two examples to get you started.

Use make to compile your tests. You will get a compilation message something like this:

 $ make tests
 ln -s /home/brody/public/cs35/s17/unittest-cpp unittest-cpp
 clang++ -g -std=c++11 -Werror -c -o tests.o tests.cpp
 clang++ -g -std=c++11 -Werror -o tests tests.o quickSort.o
   /home/brody/public/cs35/s17/unittest-cpp/CMakeFiles/UnitTest++.dir/UnitTest++/*.o
   /home/brody/public/cs35/s17/unittest-cpp
   /CMakeFiles/UnitTest++.dir/UnitTest++/Posix/*.o
      

Then execute your tests:

 $ ./tests
 Success: 6 tests passed.
 Test time: 0.00 seconds.
      

If you have bugs in your sorting algorithm, the test program will tell you which unit tests fail.

You are required to write at least four more tests that investigate different aspects of sorting. Some ideas for additional tests include:

• Sorting a large array of numbers which approach a midpoint from opposite directions (e.g. [0, 1000, 1, 999, 2, 998, ...])
• Sorting an already sorted array, and checking whether it stays that way.
• Sorting an array that contains several duplicates to make sure they are handled correctly.
• Sorting a single-element array (or an empty array!) to make sure nothing bad happens.

Although you have a minimum number of tests to write, you should ideally write as many as it takes for you to be confident in your code. Additionally, the ideal time to write your tests is prior to writing your code. Remember to rerun make tests each time you change tests.cpp.

Commenting and Coding Style Requirements

For this and future labs, graders will assign minor penalties for poor commenting and coding style. Here are some style tips for this lab:

• You should pick meaningful variable names.

    // good
    int *array = new int[size];
    // bad
    int *a = new int[size];
  

• You should use correct and consistent indentation. Lines of code within a block should be indented two spaces further than lines surrounding them.*

    //good
    if(condition) {
      cout << "Test" << endl;
    }
  
    //bad
    if(condition) {
  cout << "Test" << endl;
       }
  

  *if your text editor's default indenting is four spaces instead of two, don't stress about it. Just be consistent when indenting.
  
• You should use a code block whenever possible, even if it's not necessary. This will help you avoid subtle/messy errors in the future.

  //good
  if(condition) {
    cout << "Something" << endl;
  }
  
  //legal but bad
  if(condition)
    cout << "Something" << endl;
  			 

• Do write comments at the top of each file, indicating your name and the purpose of the code file
• You don't have to write a comment for each line of code, but do write comments about meaningful chunks of code such as a loop, if/else statement, etc.
• Do write comments describing the purpose and signature of each function declaration. use @param to describe an input parameter and @return to describe what gets returned. An example lies below:

  /**
   * Performs the main quick sort algorithm to sort the provided array.
   * @param array The array to sort.
   * @param startIndex The leftmost index (inclusive) of the part of the array
   *                   to sort.
   * @param endIndex The rightmost index (inclusive) of the part of the array
   *                 to sort.
   */
  void quickSort(int* array, int startIndex, int endIndex);
  

We've seen multiple different sorting algorithms at this point. How fast is quickSort really? Can you write a faster sorting algorithm? If you're looking for an extra challenge, try one of the following:

• Write a benchmarking program that runs similar sorting tests on quickSort, mergeSort, and whatever other sorting algorithms you want to implement and run. Which algorithm(s) are fastest in practice? Is one algorithm always faster than the rest, or are different algorithms faster in different situations?
• Try to come up with a newer faster $O(n\log n)$ sorting algorithm, and run your benchmark on this sorting implementation too.

These additional features are optional -- we'll look at them, but they won't be for credit. Make sure you complete and push the main lab before starting any extra challenge, and note in your README file that you've done extra challenges so the graders know which version of your lab to grade. (There's a chance your added features will break our grading scripts; we'll grade the base version of your lab to ensure you don't get penalized in the off-chance your extra features break our grading scripts) When you have completed your lab, answer a few short survey questions in the file README.md

To summarize the requirements of this lab:

• Your WrittenLab.pdf should contain formal proofs of the two big-O statements from Part 1.
• It should also include an analysis of the six mystery functions from part 2, along with at least two graphs to support your analysis.
• You must implement quickSort using the provided starter files and the algorithm we saw in class.
• You must test your quickSort implementation using unit tests in tests.cpp, and you must write at least four new unit tests.
• Your code and writeup must be properly commented and documented.
• You must complete the survey in the file README.md.

Once you are satisfied with your code, hand it in using git. Remember the add, commit, push development cycle. You can push as many times as you like, but only the most recent submission will be graded. You may want to run git status to confirm all modifications have been pushed.