Lab 4: QuickSort and Big-O

Due on Wednesday, October 3rd at 11:59 PM. This is a team lab. You and your assigned lab partner(s) will complete this lab together. Make sure that you are familiar with the Partner Etiquette guidelines. You may discuss the concepts of this lab with other classmates, but you may not share your code with anyone other than course staff and your lab partner(s). Do not look at solutions written by students other than your team. If your team needs help, please post on the Piazza forum or contact the instructor or ninjas. If you have any doubts about what is okay and what is not, it’s much safer to ask than to risk violating the Academic Integrity Policy.

Overview

This lab consists of three primary parts:

• Implementing and testing the QuickSort algorithm
• Proving the Big-O complexity of mathematical functions
• Analyzing and empirically testing algorithms to understand complexity

You and your partner will share a repository. The URL for your repository will be

git@github.swarthmore.edu:cs35-f18/lab04-<your-teamname>

where your-teamname is a combination of your two usernames.

Please remember that both lab partners must learn this material; it will feature prominently on your tests and final exam. Do not divide up this lab to give one team member the theory material and another member the sorting algorithm. You should be working on all parts together.

Part I: QuickSort

Source: OpenClipArt.org

Your starting repository includes the following files:

• quickSort.h/quickSort.cpp: The library for your QuickSort algorithm.
• main.cpp: A small program to use your algorithm to sort command-line arguments.
• tests.cpp: A file where you will write your unit tests.
• Makefile: The file make uses to understand how to build your project.

Files that you will need to modify are bold.

To complete this lab, you should implement the quickSort function in quickSort.cpp just as we discussed the algorithm in class. You’ll need to be careful to follow the algorithm closely and to manipulate array indices accurately. You’ll probably have bugs in your first attempt, so remember the following tools we have discussed for finding and correcting mistakes:

• gdb, the debugger that lets you step through your code a little at a time
• valgrind, the program that helps you find memory errors
• UnitTest++, the unit testing framework (which you are required to use)

Unit Tests

For this lab, you will be graded not only on whether your quickSort implementation is correct but also on whether you have properly tested it. You have been provided a couple tests to start, but you are required to write at least four more tests that investigate different aspects of sorting. Some ideas for additional tests include:

• Sorting a large array of numbers which approach a midpoint from opposite directions (e.g. [0,999,1,998,2,997,...]).
• Sorting an array that is already in order and seeing whether it stays that way.
• Sorting an array in reverse order and seeing whether it winds up sorted.
• Sorting an array that contains several duplicates to make sure that they are handled properly.
• Sorting a single-element array to make sure nothing bad happens.

Although you have a minimum number of tests to write, you should ideally write as many as it takes for you to be confident in your code. Remember: each time you change your tests, run make tests before re-running your test program.

Part II: Written Assignment

In this part of your lab, you will apply the Big-O complexity material that we have discussed in class by writing some Big-O proofs about mathematical functions.

Electronic Submissions Only

In order to complete this assignment, you will need to produce a document containing some mathematical expressions and figures. You will commit and push this document to your GitHub repository; the document may take the following forms:

• A PDF file named WrittenLab.pdf containing formatted text
• A LaTeX file named WrittenLab.tex containing formatted text

Source: OpenClipArt.org

Your team must submit the document electronically in one of these forms. In particular, you are not permitted to turn in the following (to name a few examples):

• A raw text document (regardless of formatting)
• A scan of a written document (even if the scanned document is a PDF)
• A Microsoft Word file or similar word processor document (although you may write the homework in that format and then export a PDF from it)
• A piece of paper turned in by hand

A Few Words About LaTeX

LaTeX (pronounced lah-tek or lay-tek) is a document preparation system frequently used to produce conference papers, dissertations, and other academic works (in addition to other material). With LaTeX, you code your document much as you would an HTML document or a Python program. For instance, the LaTeX code

I'm \textit{not} making this up: \(e^{i\pi} = -1\)

produces

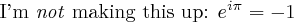
You are not required to learn LaTeX for this course. However, it may be easier to use basic LaTeX to complete your homework than to use something like Microsoft Word’s equation editor. In case you’re interested, the following files are already part of your repository:

• LearningLaTeX.tex: A LaTeX document with some examples of how to use LaTeX to write the things you need to write in this lab. You should look at the .tex file before looking at the .pdf it produces.
• WrittenLab.tex: A LaTeX document containing your homework problems and places for you to fill them in. These same problems are listed below, but they have been included in this document for your convenience.

Big-O Proofs

Use the formal definition of Big-O notation to prove the following statements:

1. \(5n^{3} - 2n^{2} + 4\) is \(O(n^{3})\)
2. \(3n^{2} + 6n\) is \(O(n^{2})\)

Part III: Mystery Functions

In this part of the lab, you will first analyze six simple loop structures and determine their runtime complexity in terms of Big-\(O\) notation. Then, using the provided program function_timer, you will graph the empirical runtimes of a these functions in a mixed up order. Your job will be to match your theoretical analysis to the empirical data.

Functions

Source: OpenClipArt.org

Begin by identifying the Big-\(O\) runtime for each of the following functions. Provide a brief justification of your answer; a sentence or two should do. Give the strictest Big-\(O\) you can find (don’t give \(O(2^n)\) if the function is also \(O(n)\)) and leave out any unnecessary terms (give \(O(n^2)\) rather than \(O(n^2+3n)\)).

• Function fnA(n)
    For i = 1..n*n
      a = i
    End For
  End Function
  

• Function fnB(n)
    k = 1
    While k < n
      For i = 1..n
        a = i
      End For
      k = k*2
    End While
  End Function
  

• Function fnC(n)
    For i = 1..n
      a = i
    End For
  End Function
  

• Function fnD(n)
    For i = 1..n
      For j = 1..i
        a = j
      End For
    End For
  End Function
  

• Function fnE(n)
    For i = 1..n
      For j = 1..i*i
        a = j
      End For
    End For
  End Function
  

• Function fnF(n)
    For i = 1..n*2
      a = i
    End For
  End Function
  

Using function_timer to Inspect the Functions

Each of the above functions has been implemented and packaged into an executable function_timer that was provided to you in your repository for this lab. The function_timer program will provide empirical runtime data for each function in a form that can be graphed by another tool called gnuplot.

To use this program, you must pick the following:

• Which function(s) to plot. For each function, you must provide a command-line argument in the form -2, -3, etc.
• The minimum and maximum values for \(n\). Remember: for slow algorithms, \(n\) should be small or the program may take a very long time. For fast algorithms, you’ll need to give a very large \(n\) or you won’t be able to see anything meaningful on the plot. Start with small \(n\) for each function and work your way up.

For instance, you can graph functions 2 and 3 within \(10 \leq n \leq 100\) by running this command:

./function_timer -2 -3 -n 10 -m 100 | gnuplot

If you get a Permission denied error when trying to run the above command, then do: chmod u+x function_timer to make this program executable, and re-try the command.

After a moment, a window will pop up with an image like this:

Note the “pipe” character (|) in the command above; this feeds the output of function_timer to the input of gnuplot so it can graph the results for you.

If you want to save the image that gnuplot makes for you, you can add a -s parameter to function_timer like so:

./function_timer -2 -3 -n 10 -m 100 -s "f2,f3 from 10 to 100.png" | gnuplot

Written Response

For this part of the assignment, include in WrittenLab.pdf the following parts:

1. A description of which mystery function (1, 2, etc.) matches which algorithm (fnA, fnB, etc.).
2. For each mystery function, a short paragraph describing why you think it matches the algorithm you named.
3. For two of the mystery functions, a graph (saved from function_timer) that supports your claims.

Summary of Requirements

You must

• Implement and test QuickSort
• Provide a PDF or LaTeX file containing the following:
  • Proofs of the Big-O complexity of the functions described above
  • A Big-O analysis of the pseudocode algorithms given above
  • A matching of these algorithms to mystery functions using function_timer