Week 9: Searching
Announcements
-
Continue working on lab 7 implementation.
Week 9 Topics
-
Search motivation
-
Linear search
-
Complexity of linear search
-
Binary search
-
Complexity of binary search
Motivation
Computer Science as a discipline is focused on two primary questions:
-
What types of problems can be solved computationally?
-
How efficiently can these problems be solved?
One of the core problems we computers are asked to solved is the search problem. Broadly speaking, the search problem searches for a query item in a potentially large set of potential matches. For two large internet companies, search is one part of their core business model.
Searching efficiently can help you solve larger problems, help more customers, or make larger profits. So how do we organize data and write code/algorithms to search efficiently? And what do we even mean by efficient?
Consider the two functions show_status_basic and show_status_hint in your guessgame_sol.py file in your w09-search folder. Each function helps play a guessing game where the computer chooses a secret number between 1 and 100 and asks the user to guess the secret number. Both count the number of guesses until you are correct. But the programs differ slightly in how they give you feedback when your guess is wrong. Try playing both games. Is one easier than the other? Do you have a different strategy for one game than the other? Why?
Linear Search
To explore the complexity of search, we will narrow the problem to searching for an item x in a python list of items. Python already has two ways of doing this. The first is the Boolean in operator, x in ls which returns True if x is in the list ls and False otherwise. Python also supports the index() method which will tell you the position in the list of the first occurrence of x, provided x appears in the list. So ls.index(x) will return an integer position if x is in ls. If x is not in the list, Python will generate an error called an exception that will likely crash your program since we have not talked much about how to handle exceptions in this class.
But how do these methods actually work? At some point, a computer scientist and python programmer designed and wrote the code for these built-in features. We will discuss the algorithm for searching a collection of items. Together, we’ll write a function
that does something familiar: search through a list for an item without using
the in operator. Our functions will be called contains and positionOf.
Complexity of Search
How do we analyze how long it takes for search to finish? We will count the steps needed to complete a task to analyze a program’s complexity. What counts as a step? What happens in the best case? Worst case? How many steps does linear search take in the worst case?
Comparing Algorithms
In addition to learning and coding a few searching and sorting algorithms over the next two weeks are going to start analyzing algorithms. We can analyze and compare algorithms by classifying them into broad complexity categories so we can compare one type of algorithm to another without worrying about details like implementation language used or speed of the physical machine.
Three algorithms to compare
To start I’ve got three algorithms to consider, which I am calling the handshake algorithm, the introductions algorithm, and the divide by 2 algorithm. Here are short descriptions of each:
-
handshake: suppose I have a class full of 34 students, and I want to meet each of my students. To do this, I walk around and say "Hi, I’m Andy" to each student and shake their hand.
-
introductions: suppose I now want to introduce each student to every other student in the class. I start by taking the first student around to every other student and introducing them. Then I go back and get the second student, take them to every other student (minus the first one, since they’ve already met), and introduce them, and so on…
-
divide by 2: suppose I divide my class into two equal parts (17 students on each side of the room), then (not sure why..) get rid of one half and repeat the process. This time I divide my 17 remaining students in half as best I can (8 on one side of the room, 9 on the other side) and again get rid of one half. I now repeat this process over and over until I have just one student left.
When deciding which algorithm to use, programmers are usually interested in three things: run time, memory usage, and storage required (disk space). If your program takes too long to run, or needs more memory than the computer has, or needs more data than can fit on the hard drive, that’s a problem.
For this class, when analyzing algorithms, we will just focus on how many "steps" or operations each algorithm requires. For the handshake algorithm above, it will obviously require 34 handshakes if I have 34 students in my class. However, to classify this algorithm, I would really like to know how the number of handshakes changes as I change the number of students in my class. For example, here’s a simple table showing number of students vs number of handshakes:
| number of students | number of handshakes |
|---|---|
34 |
34 |
68 |
68 |
136 |
136 |
272 |
272 |
Hopefully it is obvious that, if the number of students doubles, the number of handshakes also doubles, and the number of handshakes is directly proportional to the number of students.
linear algorithms: O(N)
The handshake algorithm is an example of a linear algorithm, meaning that the number of steps required, which is ultimately related to the total run time of the algorithm, is directly proportional to the size of the data.
If we have a python list L of students (or student names, or integers,
or whatever), where N=len(L), then, for a linear algorithm, the number
of steps required will be proportional to N.
Computer scientists often write this using "big-O" notation as \$O(N)\$, and we say the handshake algorithm is an \$O(N)\$ algorithm (the O stands for "order", as in the "order of a function" — more on this below).
An \$O(N)\$ algorithm is also called a linear algorithm because if you plot the number of steps versus the size of the data, you’ll get a straight line, like this:
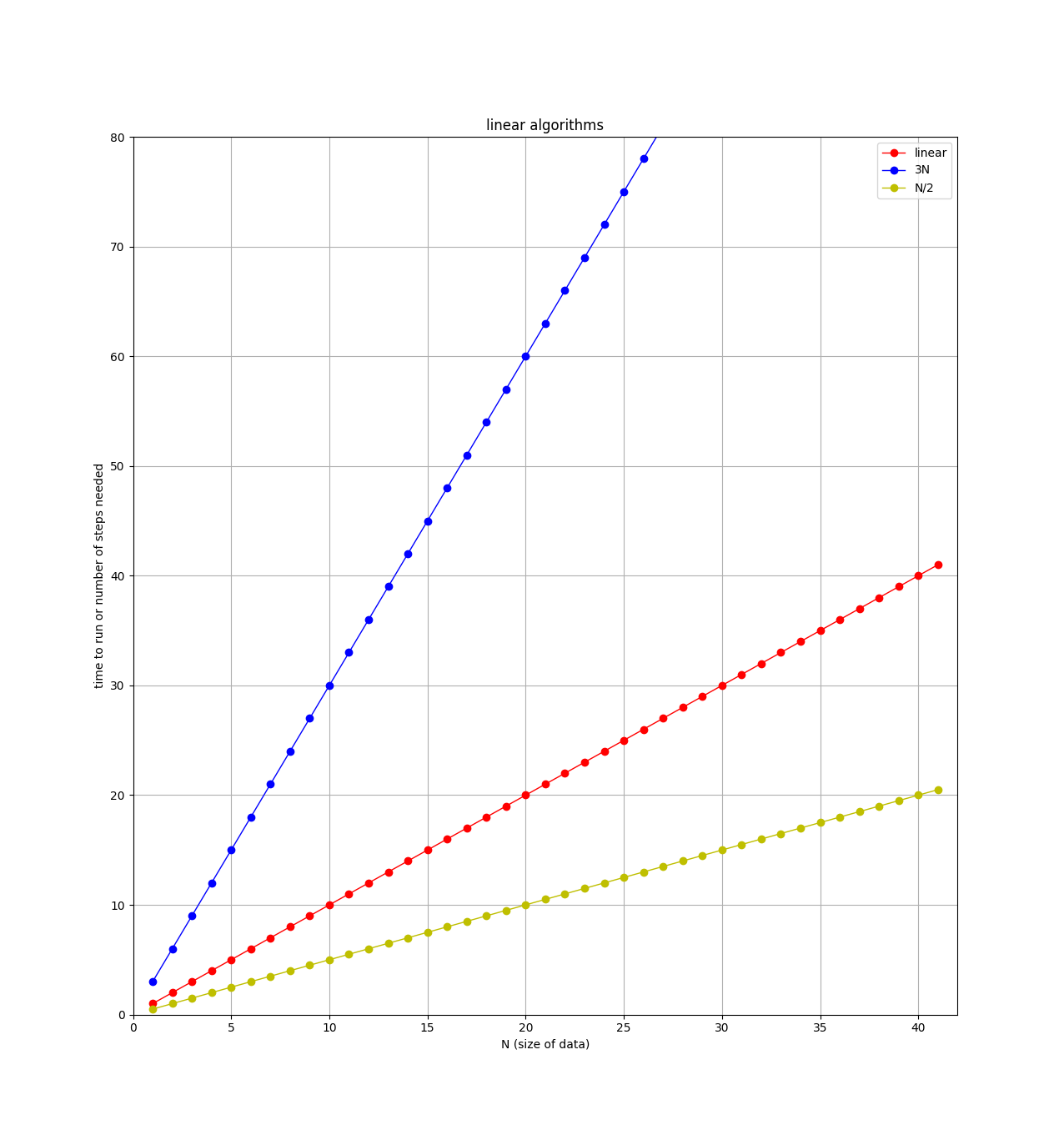
Note on the plot that there are 3 straight lines. When comparing algorithms, you might have one algorithm that requires \$N\$ steps, and another that requires \$3N\$ steps. For example, if I modify the handshake algorithm to not only shake the student’s hand, but also ask them where they are from, and write down their email address, then this algorithm requires 3 steps (shake, ask, write down) for each student. So for \$N\$ students, there would be \$3N\$total steps. Clearly the algorithm that requires the least steps would be better, but both of these algorithms are classified as "linear" or \$O(N)\$ . When classifying algorithms and using the big-O notation, we will ignore any leading constants. So algorithms with \$3N\$ steps, \$N\$ steps, \$N/2\$steps, and \$100N\$ steps are all considered as "linear".
Quadratic Algorithms: \$O(N^2)\$
For the introduction algorithm discussed above, how many introductions are required? We can count them and look for a pattern. For example, suppose I had only 6 students, then the number of introductions would be:
5 + 4 + 3 + 2 + 1 = 15
Remember, the first student is introduced to all of the others (5 intros), then the second student is introduced to all of the others, minus the first student, since they already met (4 intros), and so on.
If I had 7 students, then the number of introductions would be:
6 + 5 + 4 + 3 + 2 + 1 = 21
and if I had \$N\$ students:
\$(N-1) + (N-2) + (N-3) + ... + 3 + 2 + 1 =\$ ???
If you can see the pattern, awesome! Turns out the answer is
\$\frac{(N-1)(N)}{2}\$ introductions for a class of size N. Try it for the
N=6 and N=7 cases:
>>> N=6 >>> (N/2)*(N-1) 15.0 >>> N=7 >>> (N/2)*(N-1) 21.0
Another way to see that is with a bar chart showing how many introductions each student will make:
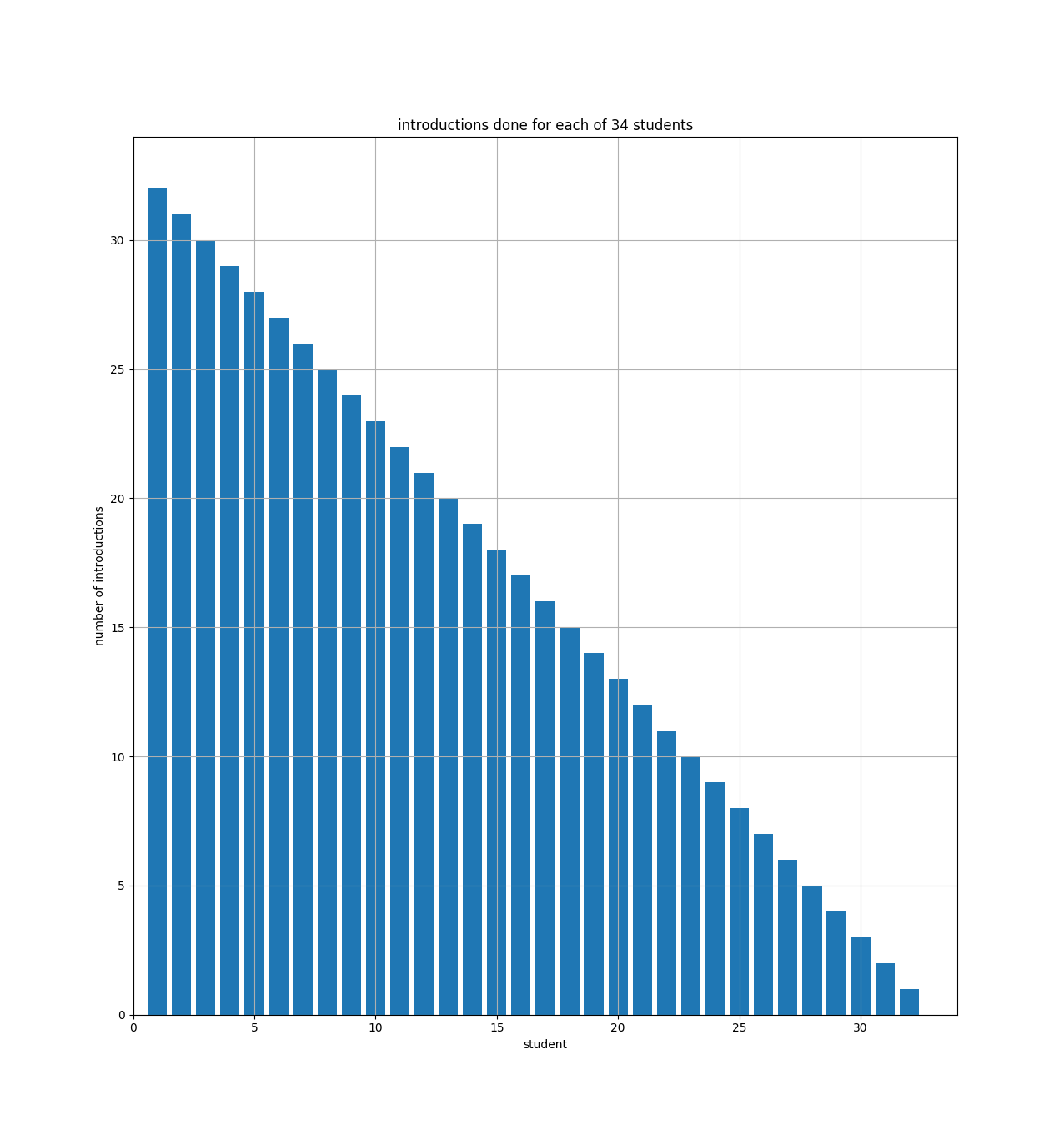
The bar chart just shows that student number 1 (on the x axis) has to do 33 introductions (the y axis), and student number 2 has to do 32, etc. And you can see how the bars fill up half of a 34x33 rectangle. So if we had \$N\$ students, the bar chart would fill up half of an \$(N-1) \times N\$ rectangle.
For the equation above \$\frac{(N-1)(N)}{2}\$, if you multiply it out, the leading term is N-squared over 2 (i.e., half of an \$N \times N\$ square).
When comparing algorithms, we are mostly concerned with how they will perform when the size of the data is large. For the introductions algorithm, the number of steps depends directly on the square of \$N\$. This is written in big-O notation as \$O(N^2)\$ (order N squared). These types of algorithms are called quadratic, since the number of steps will quadruple if the size of the data is doubled.
Here’s a table showing the number of introductions versus the number of students in my class:
| number of students | number of introductions |
|---|---|
34 |
561 |
68 |
2278 |
136 |
9180 |
272 |
36856 |
Notice how the number of introductions goes up very quickly as the size of the class is increased (compare to number of handshakes above).
logarithmic algorithms: \$O(\log N)\$
For the divide by 2 algorithm discussed above, how many times can I divide my class in two before I get down to just one student left?
To make things easier, assume I have a class of just 32 students. Then I can divide the students in two 5 times: 32→16→8→4→2→1.
We’re interested in knowing how the number of steps changes as the size of the data changes. If I double my class size to 64 students, how many more steps (divisions) will be required? The answer: just one extra division! That’s because the first division (64→32) gets us back to the class of just 32 students, and we know that only took 5 divisions, so a class of 64 will take 6 total divisions.
Again, if you can see the pattern here, awesome! If not, maybe this table will help:
| number of students | number of divisions |
|---|---|
32 |
5 |
64 |
6 |
128 |
7 |
256 |
8 |
Hopefully you can see that 2 raised to the 5th power is 32, and 2 to the
6th is 64 (try it in the python interactive shell: 2**5).
So for a class of N students, we want to know what \$x\$ is in the equation \$2^x=N\$. This is solved with a logarithm. Taking the base 2 log of \$N\$ will get you \$x\$, which you can also see using the python interactive shell:
>>> from math import log >>> log(32,2) 5.0 >>> log(64,2) 6.0 >>> log(128,2) 7.0 >>> log(1000000,2) 19.931568569324174
Finally, here’s a plot showing each type of algorithm we’ve looked at so far (plus one more we’ll see next week). All lines show number of steps (y axis) versus the size of the data (x axis).
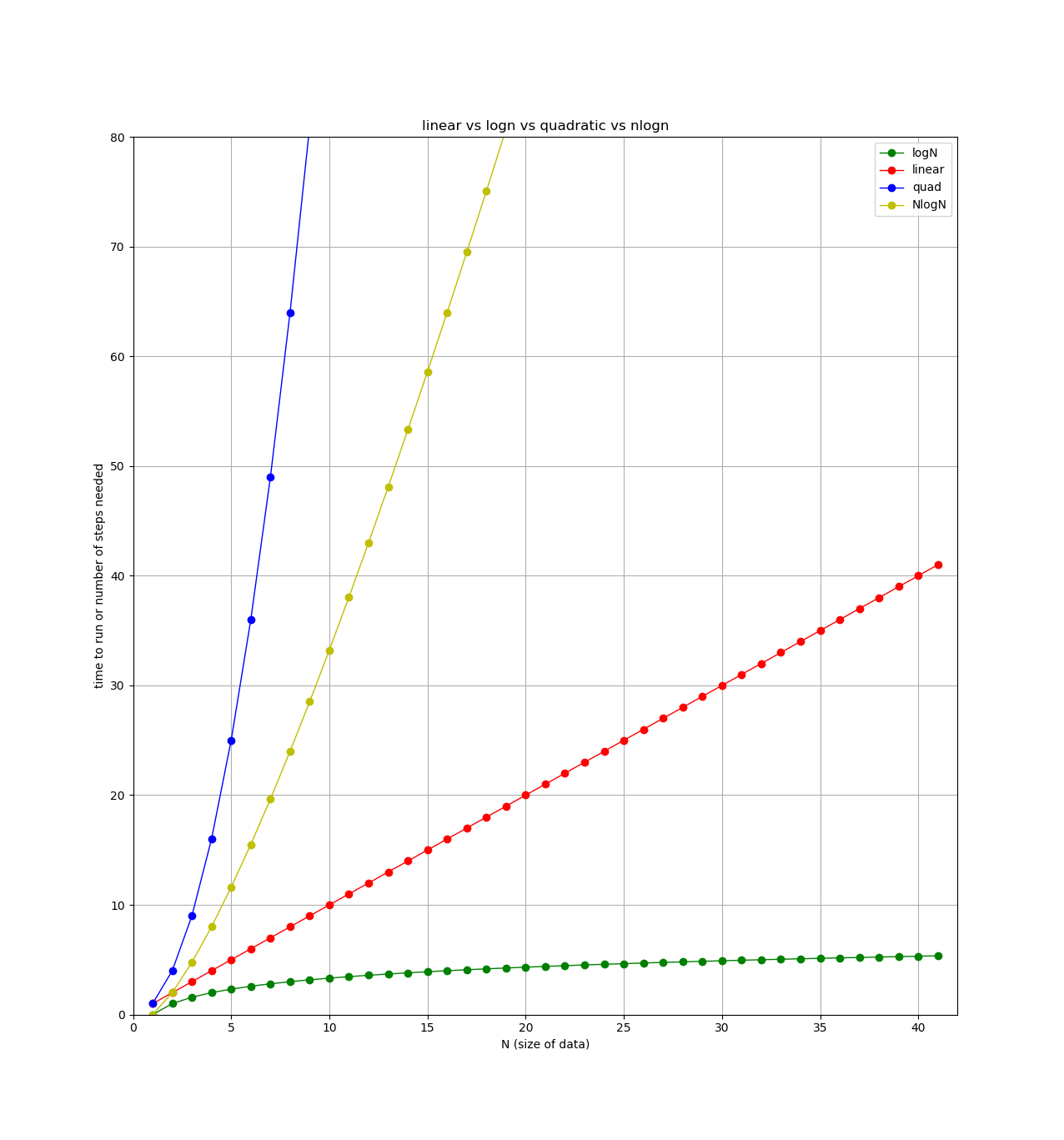
Binary Search
A key algorithmic question is: can we do better? In some cases, we can’t (and we can prove this!). In the case of linear search, we cannot do better in the general case. However, if all items in the collection are in sorted order, we can perform a faster algorithm known as binary search.
Binary search works using divide and conquer approach. Each step of the algorithm divides the number of items to search in half until it finds the value or has no items left to search. Here is some pseudocode for the algorithm:
set low = lowest-possible index
set high = highest possible index
LOOP:
calculate middle index = (low + high)/2
if item is at middle index, we're done (found it! return matching index)
elif item is < middle item,
set high to middle - 1
elif item is > middle item,
set low to middle + 1
if low is ever greater than high, item not here (done, return -1)