CS21 Lab 6: graphics

Due Saturday, October 27, before midnight

Goals

start learning about computer graphics
practice using objects and methods
practice functions and loops

Programming tips/requirements

Use the Zelle Graphics Documentation as a reference!!!!!
Same as always: header at the top, comments, good variable names, write and test incrementally
Don't hard-code values! Define variables, like width and height, then specify positions, sizes, lengths, etc. in relation to the width and height
We have provided some images below. It's okay if your images look a little different, as long as they still satisfy the program requirements described below
If you are working remotely, see our help page on remote access as well as the Piazza post about working remotely
When using input() to ask the user for input, doing that before setting up the graphics window is often easier (less clicking back and forth between windows)
Don't forget to run update21 and put your programs in your cs21/labs/06 directory

1. Circle Art

In this first program you'll create a grid of circles with blended coloring.

circles5x5

Here are a few steps and suggestions to help you get started. Computers need a coordinate system to draw. The Zelle coordinate system is two-dimensional, having an x-axis and y-axis. The x-axis goes from left to right. The y-axis goes from top to bottom. The point (0,0) is at the top, left corner. The bottom right corner has the coordinate (window width, window height). The coordinate (0,0) has a special name, called the origin. To draw a circle, you must give a coordinate which specifies the location of the center as well as a radius. We recommend drawing the Zelle coordinate system on paper and working out the coordinates of the shapes you wish to draw before you start programming.

Read the overview in the Zelle Graphics Documentation. This section includes a sample program which shows how to open a window and draw a circle. Copy this code into circle.py and verify that it works. This program draws a circle at coordinate (50,50) and radius 10. Verify that the size and position of the circle makes sense. Note that clicking on the window closes it.
For this question we will always have a square window of size 400. Modify circle.py so the window width and height are 400. To figure out how, look up the function definition for GraphWin(...) in the Zelle manual.

$ python3 circle.py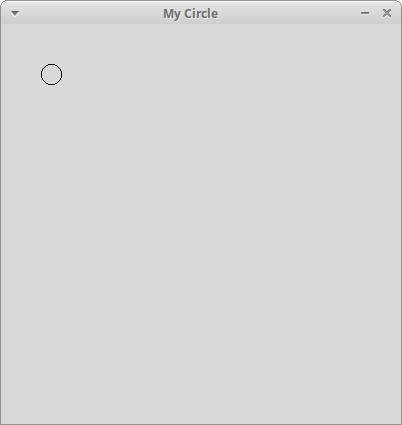

circles_tutorial

Try setting the background to white using the function setBackground(...). Look up the function in the Zelle manual for an example to help you.

$ python3 circle.py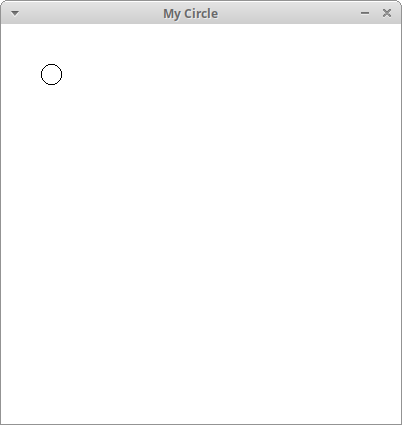

circles_background

Ask the user for the number of circles to draw along each row and column. Eventually, we will draw a grid of circles but to start, we will draw a single circle at the top left. Our first step is to compute the radius. We will make the radius an integer so our loops are easier to write. To compute the radius, divide the window size by the number of circles to get the diameter. The radius is then half the diameter. Modify your program to compute an x and y coordinate for a circle with your computed radius. The circle should be flush against the top left corner.

$ python3 circle.py 
Please enter a number of circles for the width and height: 5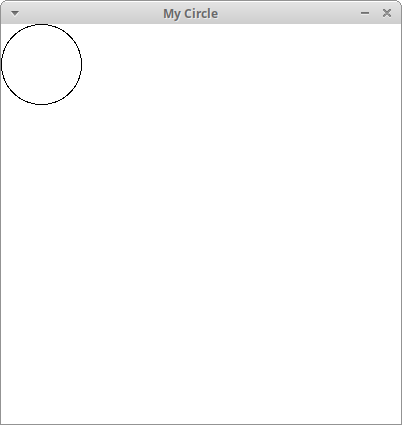

circles_single

Next, draw a single row of circles across the top. Modify main() to create circles in a loop. What should the y coordinate of these circles be? How should the x coordinates change? Write your ideas on paper before coding.

$ python3 circle.py 
Please enter a number of circles for the width and height: 5

circles5x5_row1

To draw a grid of circles, we will need a nested loop. The outer loop will change the coordinates of the columns (e.g. x as before). The inner loop will correspond to rows (e.g. by changing y). Hint: The y coordinate should change in the same way as x!

$ python3 circle.py 
Please enter a number of circles for the width and height: 5

circles5x5_grid

Now that you have a grid of circles, try setting a color for your circles using the function setFill(...). Colors in Zelle are represented either with strings or with (red, blue, green) tuples of integers ranging from 0 to 255. For example, the color yellow is represented as either color_rgb(255,255,0) or as the word "yellow". The color blue is color_rgb(0,0,255) or the word "blue". See here to get tuples for different colors. In the example below, we fill the circle with the color "cyan" which is (0,255,255)

$ python3 circle.py 
Please enter a number of circles for the width and height: 5

circles5x5_cyan

Last step! Define a function getColor(px,py,winSize) to generate a color for each circle based on its position using a gradient. Your function should take the circle center (px, py) and the window size as arguments and return the color. Then pass this color to the function setFill(..). Recall that a color is a tuple of (red, green, blue). We can add and scale colors to create new colors! The only constraints are that
the final rgb color values are all between 0 and 255
the final rgb color values are integers

To create a horizontal gradient, we will blend between two colors based on the x-coordinate of the circle's center. When x is close to zero (the left-side of the screen), the circles will have the first color. When x is close to the window's width (the right-side of the screen), it will have the second color. When x is half the window width, the color will be 50% of the first color and 50% of the second color. Let our first color be C₁ = [R₁, G₁, B₁]^T, our second color be C₂ = [R₂, G₂, B₂]^T, and the percentage distance along the X-axis be α. The general formula for this gradient is
$$ \left[\begin{array}{c} R \\ G \\ B \end{array} \right] = (1 - \alpha) \left[\begin{array}{c} R_{1} \\ G_{1} \\ B_{1} \end{array} \right] + \alpha \left[\begin{array}{c} R_{2} \\ G_{2} \\ B_{2} \end{array} \right] = \left[\begin{array}{c} (1 - \alpha) R_{1} + \alpha R_{2} \\ (1 - \alpha) G_{1} + \alpha G_{2} \\ (1 - \alpha) B_{1} + \alpha B_{2} \end{array} \right] $$
Let's start by breaking down what this formula means:

multiply each R,G,B value in the first color by (1 − α)
multiply each R,G,B value in the second color by α
add pairwise the components of each color

Now let's look at some examples. Suppose our window size is 400. What is the color of a circle at location (0,0)? α will be 0/400 = 0, or 0% across the window. Now suppose our first color C₁ is yellow [255, 255, 0]^T and our second color C₂ is blue [0, 0, 255]^T. In this case, the gradient color is 100% of the first color and 0% of the second color, which we can see by plugging in our values

$$ \left[\begin{array}{c} 255 \\ 255 \\ 0 \end{array} \right] = (1 - 0) \left[\begin{array}{c} 255 \\ 255 \\ 0 \end{array} \right] + 0 \left[\begin{array}{c} 0 \\ 0 \\ 255 \end{array} \right] $$

Now suppose we have a circle at position (400,0). Now α is 400/400 = 1, or 100% across the window. When we plug in our values, we see that we get 0% of the first color and 100% of the second color.

$$ \left[\begin{array}{c} 0 \\ 0 \\ 255 \end{array} \right] = (1 - 1) \left[\begin{array}{c} 255 \\ 255 \\ 0 \end{array} \right] + 1 \left[\begin{array}{c} 0 \\ 0 \\ 255 \end{array} \right] $$
Verify for yourself that a circle at position (200,0) will be 50% of C₁ and 50% of C₂. You may use any colors you like. The following screenshot uses the colors yellow and blue.

$ python3 circle.py 
Please enter a number of circles for the width and height: 5

circles5x5

$ python3 circle.py 
Please enter a number of circles for the width and height: 50

circles50x50

2. Aquarium

Write a program called aquarium.py that generates an animated aquarium, using mouse-clicks from the user. Here is an example:

Here are the requirements and some tips for this program:

Create a fixed sandy ground using a Rectangle (not based on user clicks).
Create and update a Text object that tells the user what to do in each step. The setText(<string>) method can be used to change the text at each step. The input string can also be the empty string.
Create a function that makes and draws one small fish at a given Point. The fish in the video were created using a polygon. The five points of the polygon are computed relative to the given point (px, py). Δx and Δy are distances that you can hard-code. The numbers beside each to point is a suggested order that you can give them to the Polygon(...) constructor.

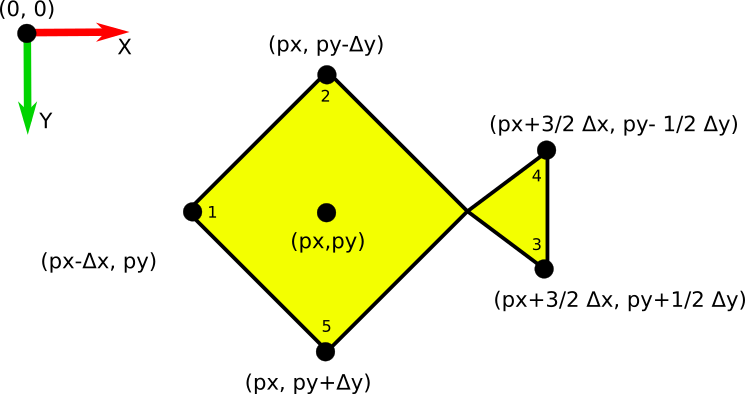
Your fish does not have to look exactly like these fish. Feel free to personalize them.

In main(), use a while loop to let the user click to create multiple fish. Whenever the user clicks, call your fish function and pass the user's click Point as an argument. When the user clicks on the ground, the while loop should end.
In main(), after creating the small fish, ask the user for a point to create a giant fish. (Note: It's possible to create your large fish in main(). However, try to think about how you can modify your fish function to create either small fish or large fish.) Write a loop to move the giant fish across the screen. To animate, call the function move(..). You can choose to iterate the animation for a fixed number of frames, or you can exit the loop on mouse click using the function checkMouse().
Finally, when the user next clicks, exit and close the window.

Aquarium Challenge! (no points...just for fun, if you have time)

There are many ways to extend this animation.

Use different colors to create a different scene, or make more elaborate composite objects.
Create a more elaborate background
Animate multiple objects in the screen
Allow the giant fish to wrap to the other side of the screen
Use random numbers to generate colors for either the fish or background objects
Use a gradient to generate colors
Play with different types of Zelle primitives
Use different formulas to animate the big fish (Idea: Use math.sin() to make your fish swim up and down)
Zelle supports png, ppm, and gif images. Try integrating images into your solution! (Hint: png supports transparency for making fish!)

Here are some sample videos with ideas

Gradient Challenge! (no points...just for fun, if you have time)

$ python3 circle.py 
Please enter a number of circles for the width and height: 5

circles5x5

In circle.py, modify your getColor(..) function to do a two-way gradient. In this case, we blend in both the X and Y directions and can use up to four colors! You can think of the two-way gradient like so:

first we blend along the X direction using the first two colors (same as before) to produce a color C_x1;
we blend again along the X direction using the second two colors (same as before) to produce a color C_x2;
to get our final color, we blend C_x1 and C_x2 in the Y direction.

$$ \left[\begin{array}{c} R_{x1} \\ G_{x1} \\ B_{x1} \end{array} \right] = (1 - \alpha_x) \left[\begin{array}{c} R_{1} \\ G_{1} \\ B_{1} \end{array} \right] + \alpha_x \left[\begin{array}{c} R_{2} \\ G_{2} \\ B_{2} \end{array} \right] $$

$$ \left[\begin{array}{c} R_{x2} \\ G_{x2} \\ B_{x2} \end{array} \right] = (1 - \alpha_x) \left[\begin{array}{c} R_{3} \\ G_{3} \\ B_{3} \end{array} \right] + \alpha_x \left[\begin{array}{c} R_{4} \\ G_{4} \\ B_{4} \end{array} \right] $$

$$ \left[\begin{array}{c} R \\ G \\ B \end{array} \right] = (1 - \alpha_y) \left[\begin{array}{c} R_{x1} \\ G_{x1} \\ B_{x1} \end{array} \right] + \alpha_y \left[\begin{array}{c} R_{x2} \\ G_{x2} \\ B_{x2} \end{array} \right] $$

For example, to get the screenshot above, we let

α_x be the percentage along X (e.g. px/winSize),
α_y be the percentage along Y (e.g. py/winSize),
C₁ be the top left color (black, e.g. [0, 0, 0] )
C₂ be the top right color (yellow, e.g. [255, 255, 0] )
C₃ be the bottom left color (blue, e.g. [0, 0, 255] )
C₄ be the bottom right color (white, e.g. [255, 255, 255] )

Mandelbrot Challenge! (no points...just for fun, if you have time)

Create a new program, mandelbrot.py, that colors circles based on the Mandelbrot set. For this challenge, you should modify circle.py so that getColor(px, py, winSize) uses the Mandelbrot formula to compute a color for each circle.

To start, modify getColor(px, py, winSize) to return white if we're outside the set and black otherwise. A point (px,py) is inside the set based on an "escape condition". We start by computing offsets (x0, y0) based on the circle center (px,py). We then initialize a pair (x,y) = (0,0) and repeatedly update the values (x,y) in a loop. If $ x^2 + y^2 $ becomes greater than 4, the point escapes (!) and we assign it a white color. Otherwise, we assume it is part of the Mandelbrot set, and we assign it a black color. The full pseudocode for getColor is below

    x0 = (px/winSize)*2.25 - 1.5
    y0 = (py/winSize)*2 - 1
    x = 0.0
    y = 0.0
    iteration = 0
    max_iteration = 1000

    while x*x + y*y < 2*2 and iteration < max_iteration
        xtemp = x * x - y * y + x0
        y = 2*x * y + y0
        x = xtemp
        iteration = iteration + 1

    if iteration < max_iteration
       return white
    else:
       return black

The following image shows the result of a size 400 window with 200 circles

You can make a more colorful visualization of the Mandelbrot set by defining a palette. A palette is a list of colors, one for every possible iteration that a point (px,py) can escape. To define a palette, create a list in main() and add 1000 random colors to it using a loop. A random color can be generated using random.randrange(255) to generate red, green, and blue color components. Then modify getColor() to take your palette as a fourth parameter. When iteration is less than 1000, use the color from your palette. Otherwise, return black as before.

Below is an example using a size 400 window with 200 circles.

3. Answer the Questionnaire

Each lab has a short questionnaire at the end. Please edit the QUESTIONS-06.txt file in your cs21/labs/06 directory and answer the questions in that file.

Turning in your labs....

Don't forget to run handin21 to turn in your lab files! You may run handin21 as many times as you want. Each time it will turn in any new work. We recommend running handin21 after you complete each program or after you complete significant work on any one program.