Consider the following code:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
"""
This program will ask the user to enter the side lengths
of a rectangle.

Two functions will be used to compute the area and perimeter
of the rectangle.

The area and perimeter will be printed back to the user.
"""
def perimeter_rectangle(length, width):
    """
    Compute the perimeter of a rectangle
    Args:
        length (int): the length of the rectangle
        width (int): the width of the rectangle
    Returns:
        int: the perimeter of the rectangle
    """
    computed_perimieter = (length + width) * 2
    return computed_perimieter

def area_rectangle(length, width):
    """
    Compute the area of a rectangle
    Args:
        length (int): the length of the rectangle
        width (int): the width of the rectangle
    Returns:
        int: the area of the rectangle
    """
    computed_area = length * width
    return computed_area

def main():
    print("Let's compute data about a rectangle!")
    side_one = int(input("Enter length: "))
    side_two = int(input("Enter width: "))

    area = area_rectangle(side_one, side_two)

    # STOP DRAWING: show the stack before we run the next line
    perimeter = perimeter_rectangle(side_one, side_two)

    print("The area is %d" % (area))
    print("The perimeter is %d" % (perimeter))

main()

Let’s draw the stack:

  1. Draw the empty stack and the heap.

  2. When a function is called, create a stack frame for the function and put the frame on top of the stack. Usually, the first function called is main.

    1. Allocate parameters, if any, on the stack. The main function typically does not have parameters but many other functions do.

    2. Allocate variables used in the function. NOTE: For very large programs, you may want to skip drawing loop variables because they change frequently and can clutter your diagram. However, you should get in the habit of including them until you are comfortable enough to understand when they can be excluded. A loop variable is:

      for <loop_variable> in <sequence>:
	   <statements>
	   ...

    3. Execute the function line-by-line.

      • If another function is called, repeat at step 2.

      • If the function has a return value, we say that the function evaluates to be that value. Be sure to set the variable in the calling function to the returned value, if applicable.

    4. When you reach the end of the function, remove it from the stack.

  3. Continue executing the function that is now on top of the stack. If the stack is empty, the program is complete.

Below are the steps for drawing the stack for the code shown above. Line numbers are included so you can see how each line impacts the drawing. Try drawing the stack yourself and see if you get the same drawing!

Step Line # What happens to the stack diagram

0

Create the stack and the heap.
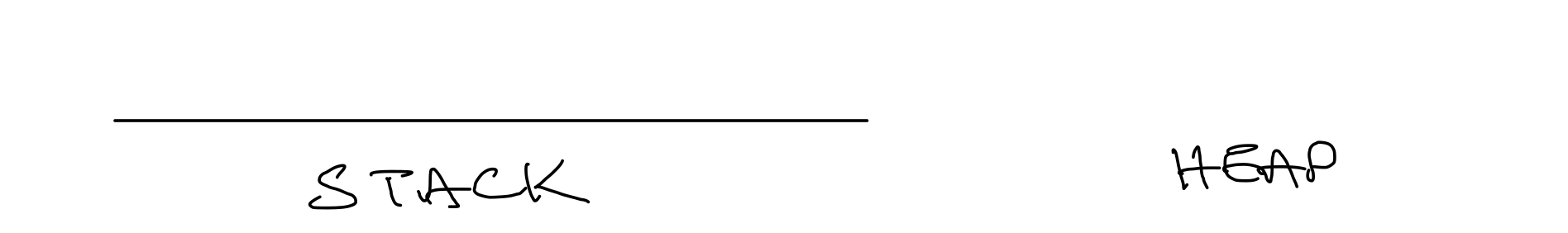
rect01
Figure 1. Stack Diagram after step 0.

1

47

Put a frame for main on the stack.
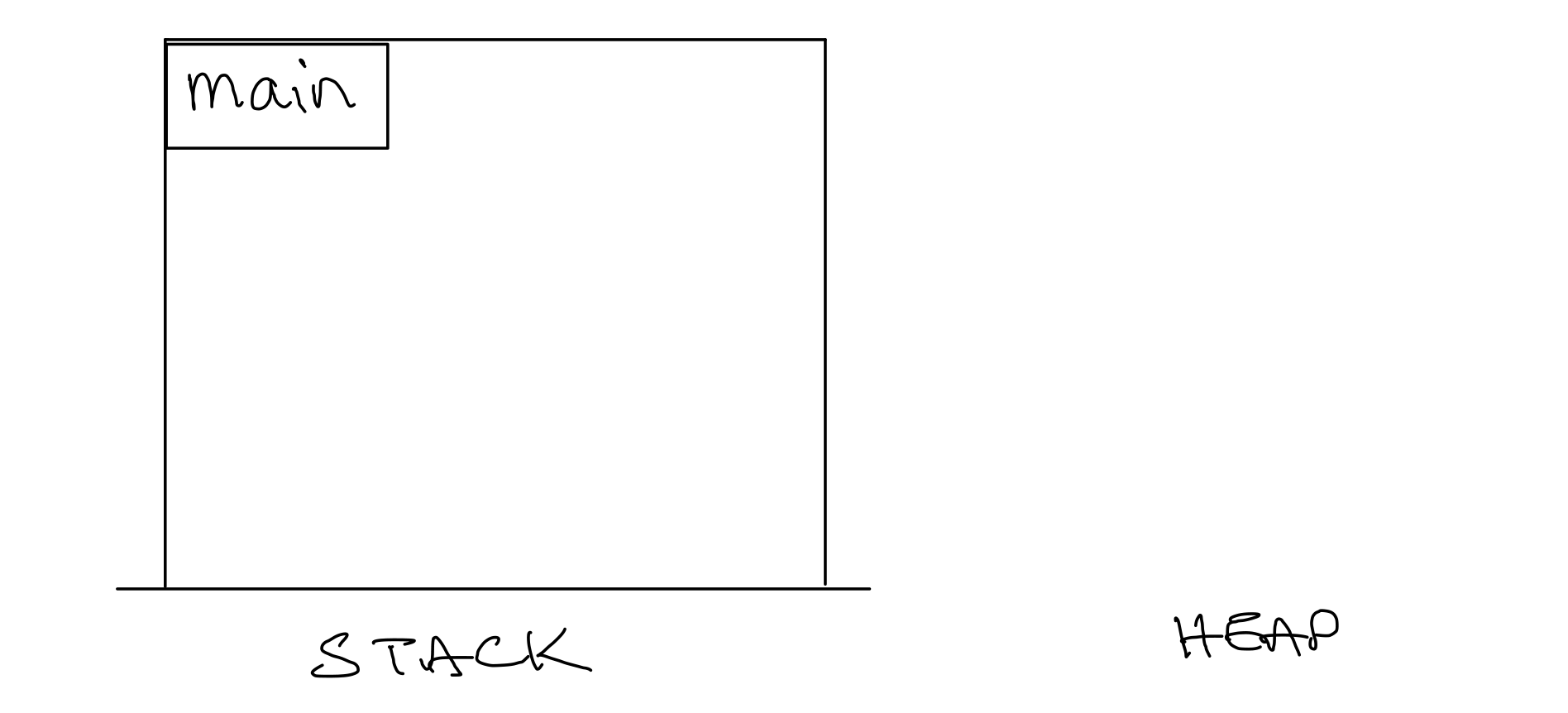
rect02
Figure 2. Stack Diagram after step 1.

2

35

Put the variables side_one, side_two, area, and perimeter in the stack frame for main.
rect03
Figure 3. Stack Diagram after step 2.

3

36-37

Assume that the user types 3 for side_one and 5 for side_two. Draw arrows from the variables side_one and side_two to 3 and 5, respectively.
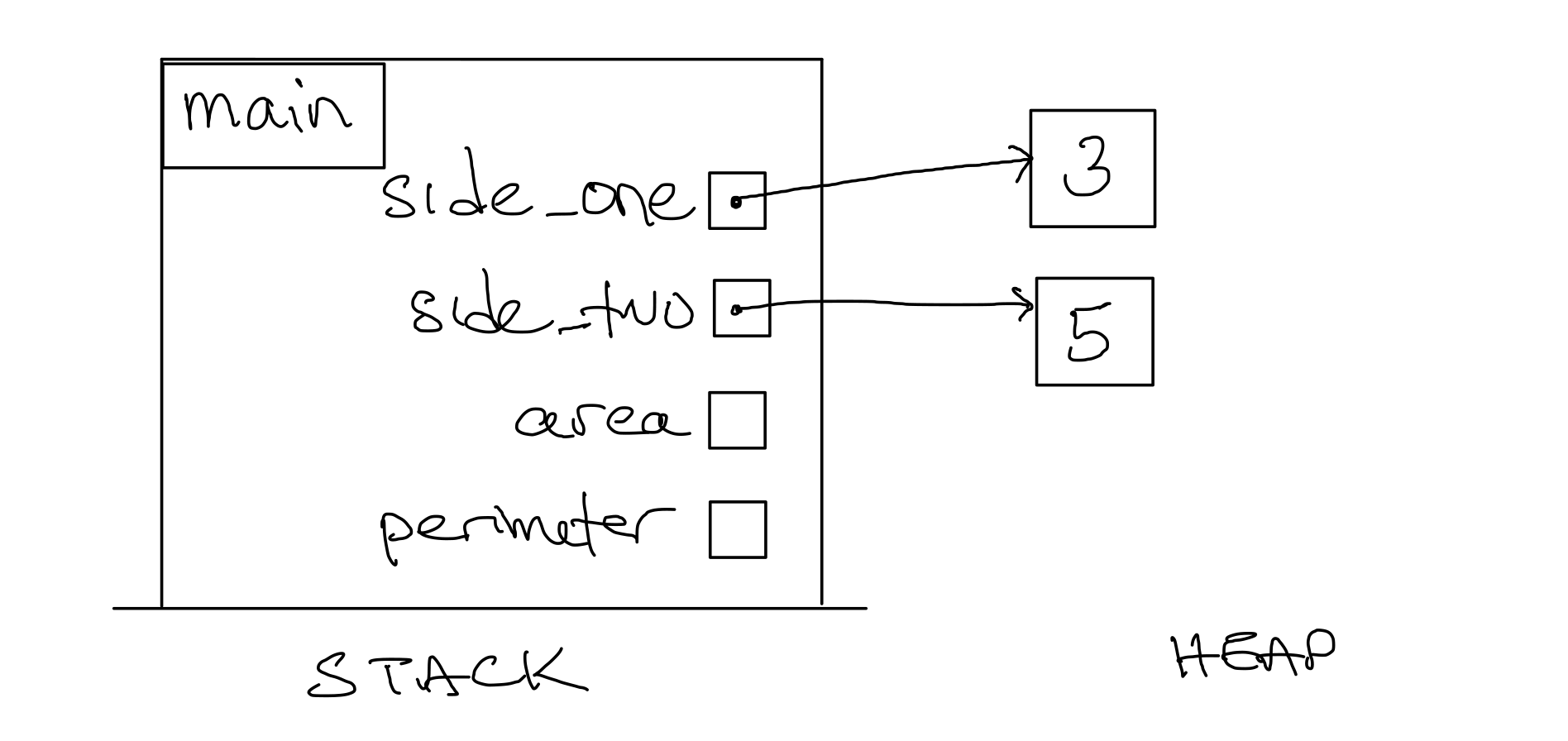
rect04
Figure 4. Stack Diagram after step 3.

4

22

The area_rectangle function is called, so we make a stack frame for area_rectangle and put it on top of the stack.

5

22

Put parameters length and width in the stack frame for area_rectangle. We also put the local variable computed_area in the stack frame.
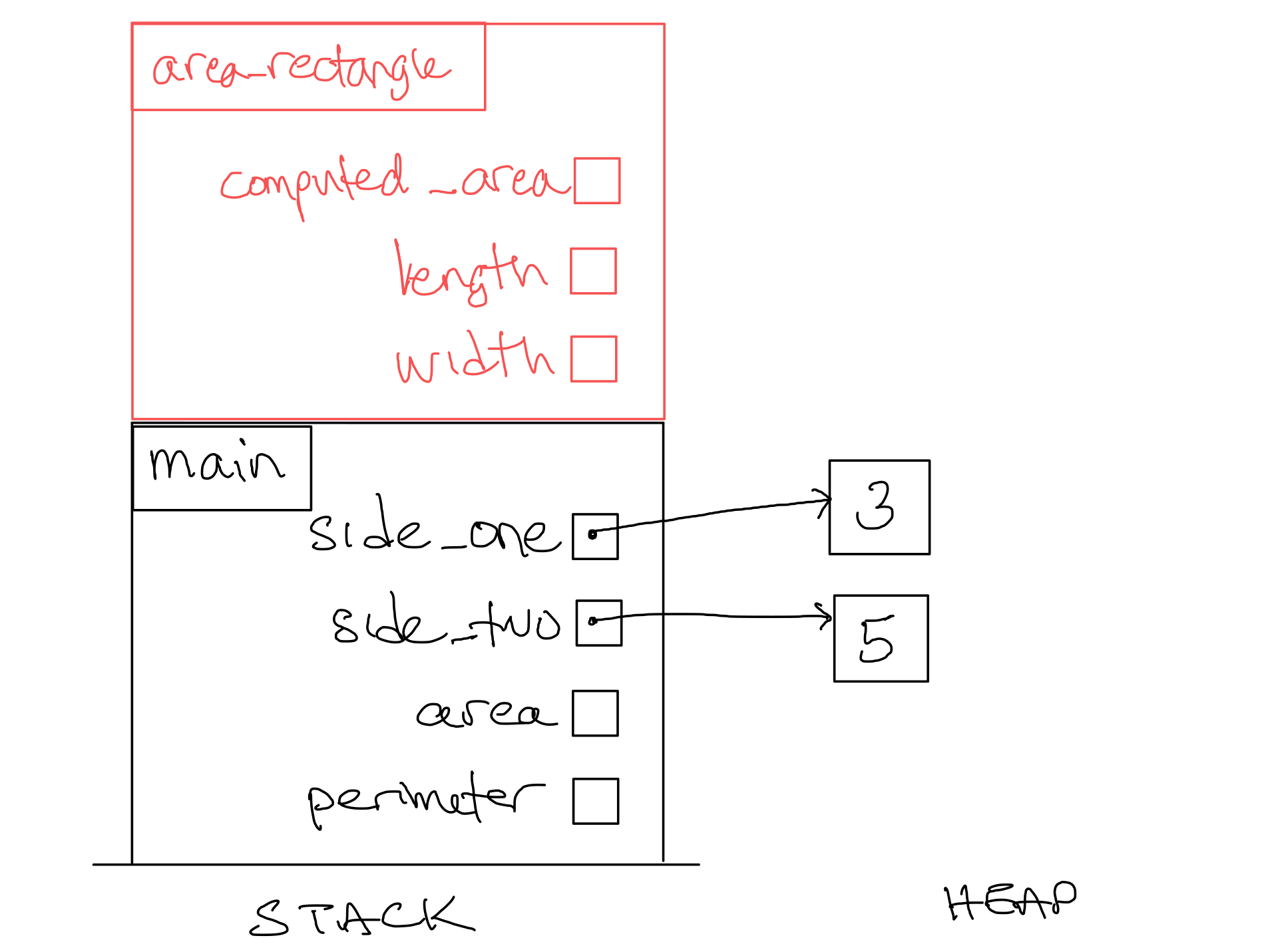
rect05
Figure 5. Stack Diagram after step 5.

6

22

We assign the first parameter, length, to be equal to the first argument, side_one. Draw an arrow from length to the same value as side_one.

7

22

We assign the second parameter, width, to be equal to the second argument, side_two. Draw an arrow from width to the same value as side_two.
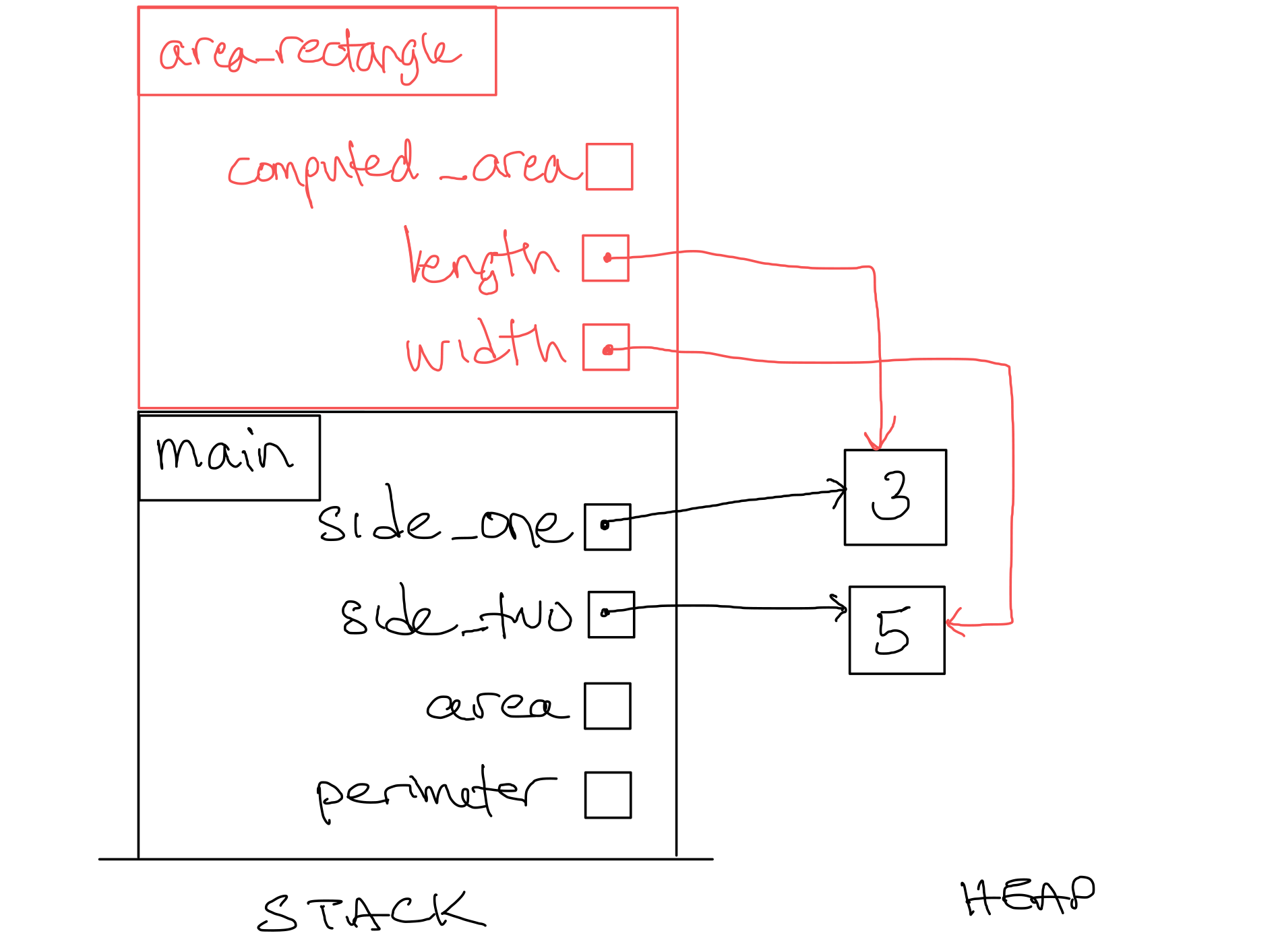
rect06
Figure 6. Stack Diagram after step 7.

8

31

Calculate length * width and draw an arrow from computed_area to that value on the heap.
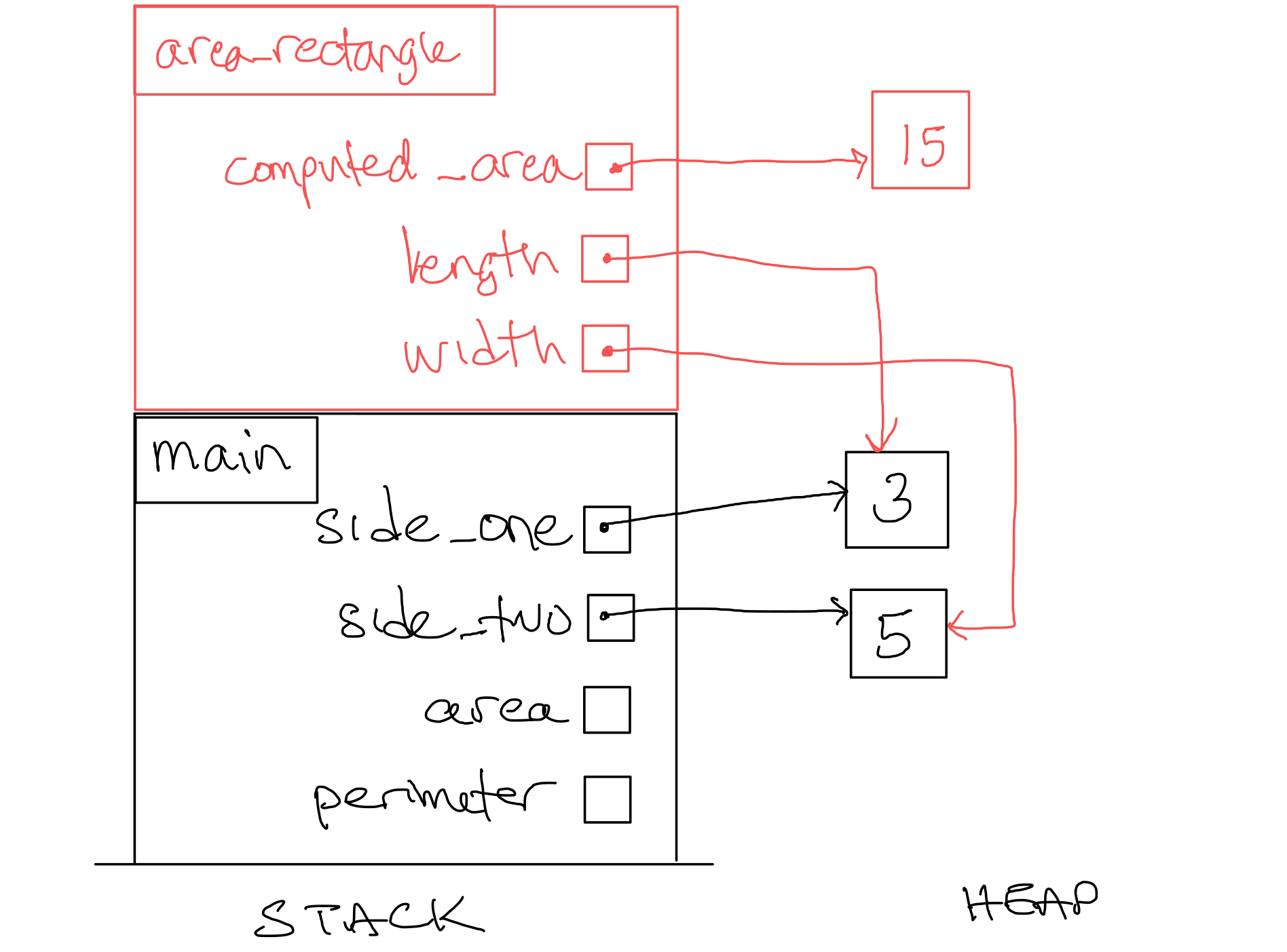
rect07
Figure 7. Stack Diagram after step 8.

9

32

We reach the return value at the end of the function. Keep track of the value being returned (shown here with the purple arrow). We say that the area_rectangle function evaluates to the value 15.
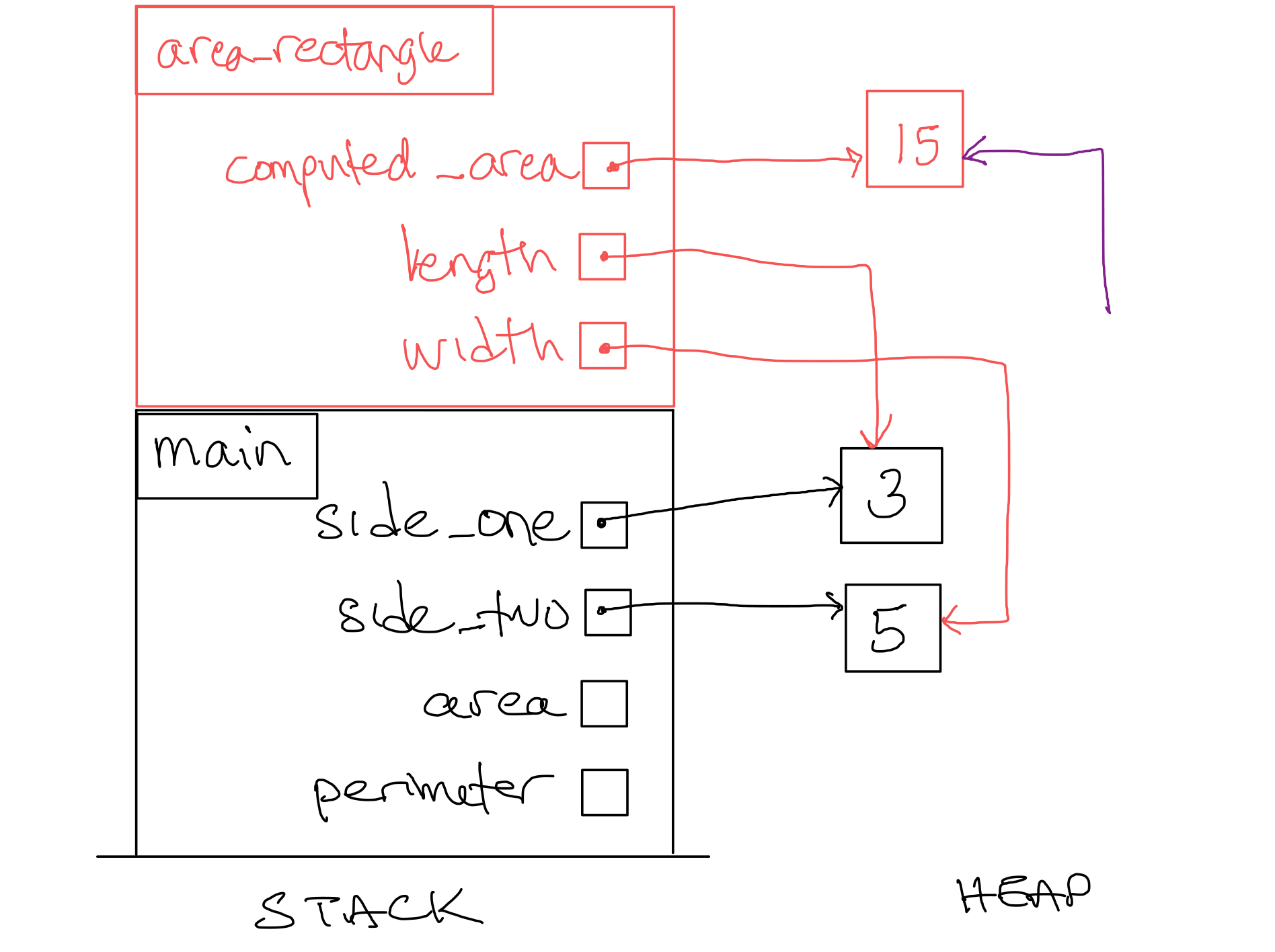
rect08
Figure 8. Stack Diagram after step 9.

10

39

Since the function is complete, we remove the stack frame for area_rectangle and we assign the returned value to the variable area.
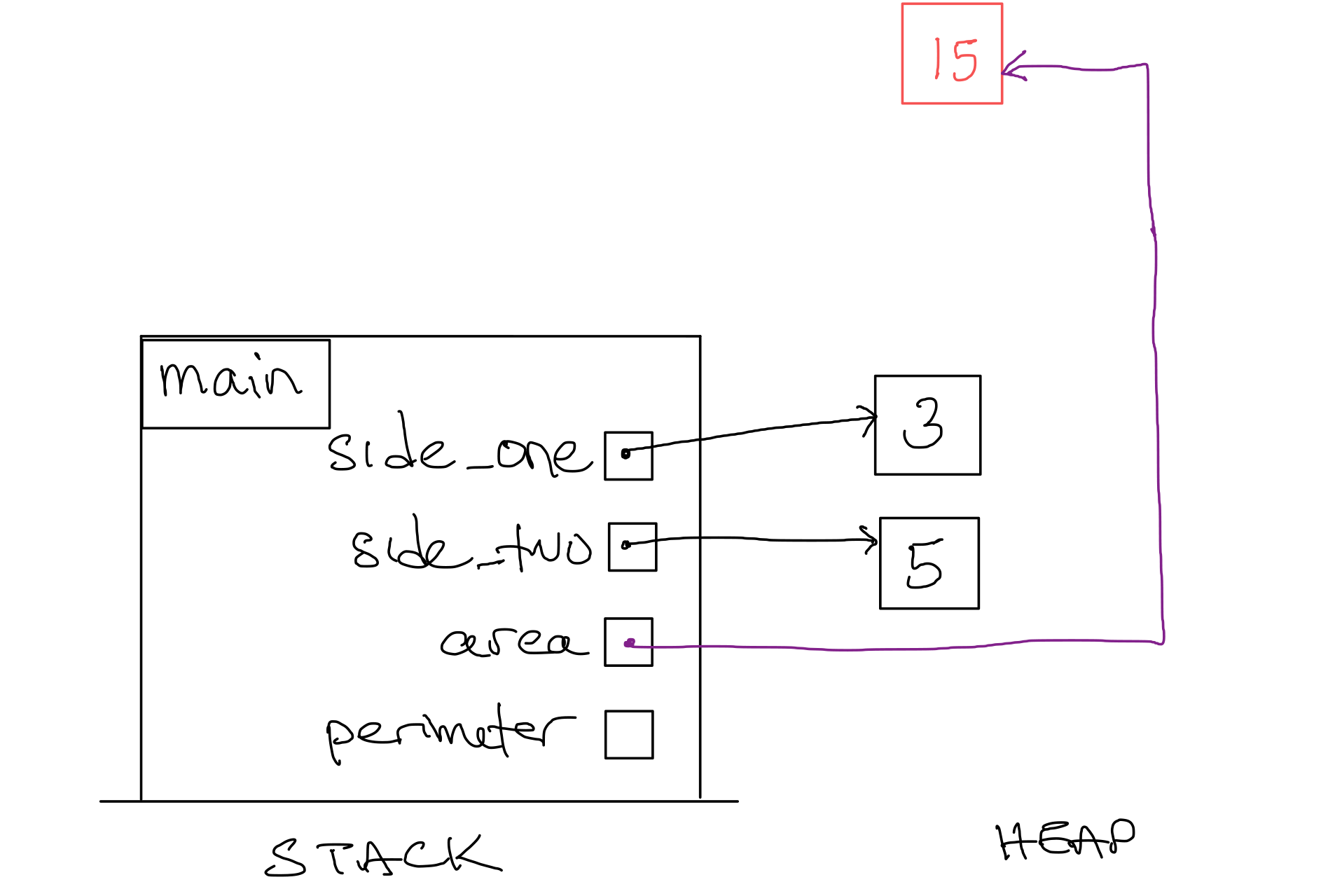
rect09
Figure 9. Stack Diagram after step 10.

11

42

Can you continue drawing the stack diagram starting on line 42?