CS21 Lab 10: Recursion

Part 1 is due on Monday, December 1 at the start of class. You must submit Part 1 on paper. Be sure that your paper is legible!
Part 2 is due on Tuesday, December 2, by 11:59am and will be turned in the "normal" way using handin21.

Goals

The goals for this lab assignment are:

Practice tracing recursive functions
Designing recursive functions
Identifying base and recursive cases

1. Tracing: Stack Diagrams

The first part of this lab asks you to read three recursive functions. For each function, complete the following steps on paper.

Identify the base case and recursive case.
Trace the programs, and drawing the stack diagrams right up until the you reach the first return statement. Do not erase stack frames as you go along.
Write down the final output of the program.

Example Question

Given the Python program shown below:

def fact(n):
    if n <= 1:
       return 1
    else:
       f = n * fact(n - 1)
       return f

def main():
   v = fact(4)
   print(v)

main()

Example Solution

Base case: when n <= 1
Recursive case(s): when n > 1
The stack diagram would look like this if we didn’t erase stack frames and ran the program to completion:
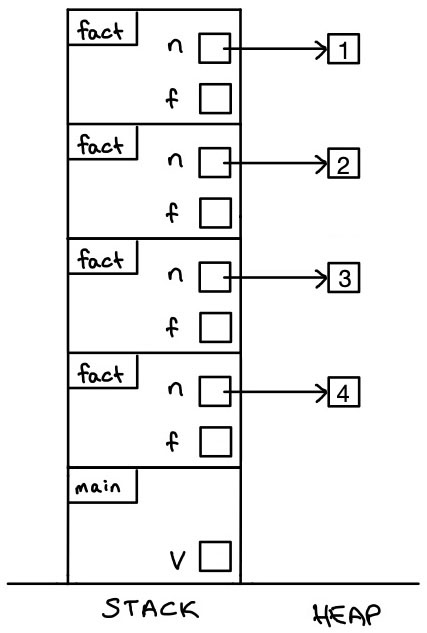
The final output of this program is:
```
Output:
24
```

Program 1

Provide the base case, recursive case, final output, and draw the stack diagram for the program shown below.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14 def main():
    reverse("cat")

def reverse(msg):
    n = len(msg)
    if n == 0:
        print("done")
        #draw stack here
        return
    else:
        reverse(msg[1:])
        print(msg[0])

main()

Program 2

Provide the base case, recursive case, stack, and final output, for the program shown below.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16 def main():
    v = mystery(15, 12)
    print(v)

def mystery(a, b):
    if b == 0:
        ans = a
        #draw stack here
        return ans
    else:
        x = b
        y = a % b
        ans = mystery(x, y)
        return ans

main()

Program 3

Provide the base case, recursive case, draw the stack diagram, and show the final output for the program shown below.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18 def main():
    nums = [4, 1, 6, 3]
    result = puzzle(nums)
    print(result)

def puzzle(ls):
    if ls == []:
        r = 0
        # draw stack here
        return r
    else:
        val = ls[0]
        r = puzzle(ls[1:])
        if val % 2 == 1:
            r = r + 1
        return r

main()

2. Designing Recursive Functions

For this part of the lab, you will design and implement recursive functions.

When designing recursive programs, identify the base case(s) first: the simplest case where there is not a recursive call. Then move on to the recursive case(s).

Replace vowels

In the file vowels.py, write a recursive function called replace_vowels(s, ch) that takes a string s and a character ch, and returns a new string that has all lowercase vowels in s replaced with the character ch. You can ignore capital vowels and assume 'y' is never a vowel: (that is, for this problem, "vowel" means only lowercase 'a', 'e', 'i', 'o', or 'u').

Be sure that your solution includes a main function that tests your replace_vowels function with a few different parameter values.

Your solution must be recursive.

def replace_vowels(s, ch):
    """
    Return a string which is a copy of `s` with all vowels replaced by the
    character specified by `ch`.
    Parameters:
        s (str): a string
        ch (str): a single character, to replace vowels with
    Returns:
        str: a copy of s, but with vowels replaced by the character `ch`
    """

For example:

print(replace_vowels("computer science is fun", "*")) # c*mp*t*r sc**nc* *s f*n
print(replace_vowels("Happy Thanksgiving!", "@")) # H@ppy Th@nksg@v@ng!
print(replace_vowels("For Good", "a")) # Far Gaad
print(replace_vowels("I LOVE RECURSION", "7")) # I LOVE RECURSION

Digit Sum

In the file digit_sum.py write a recursive function called sum_digits(n) that takes a non-negative integer n and returns the sum of its digits. Your solution must be recursive.

print(digit_sum(123)) #6
print(digit_sum(1)) #1
print(digit_sum(0)) #0
print(digit_sum(1024)) #7
print(digit_sum(97653)) #30

def digit_sum(n):
    """
    This function takes a number n and returns the sum of its digits
    Parameter
        n (int): a non-negative integer whose digits to sum
    Returns:
        int: The sum of the digits of n
    """

Hint: The last digit of a number n can be found by calculating n % 10, and the remaining digits are given by n // 10.

A Recursive Triangle Drawing

In the file triangle.py, we have given some starter code to set up a graphics window and draw a triangle with the points p1, p2, and p3. You will implement the function triangle_recursion(win, p1, p2, p3, levels), which will draw a pattern within the triangle recursively. The parameters this function takes are win, the window to draw on, the points p1, p2, p3 specifying the points of a triangle, and levels, specifying the number of levels of the pattern we want to draw. The pattern this function should draw is described below.

When the number of levels is 0, the pattern is just a triangle.

When the number of levels is larger than 0, the following happens:

We first find the midpoints of each side of the triangle (that is, the midpoint between p1 and p2, between p2 and p3, and between p1 and p3). The midpoints are shown labeled in the diagram below (where, e.g., mid12 is the midpoint of p1 and p2):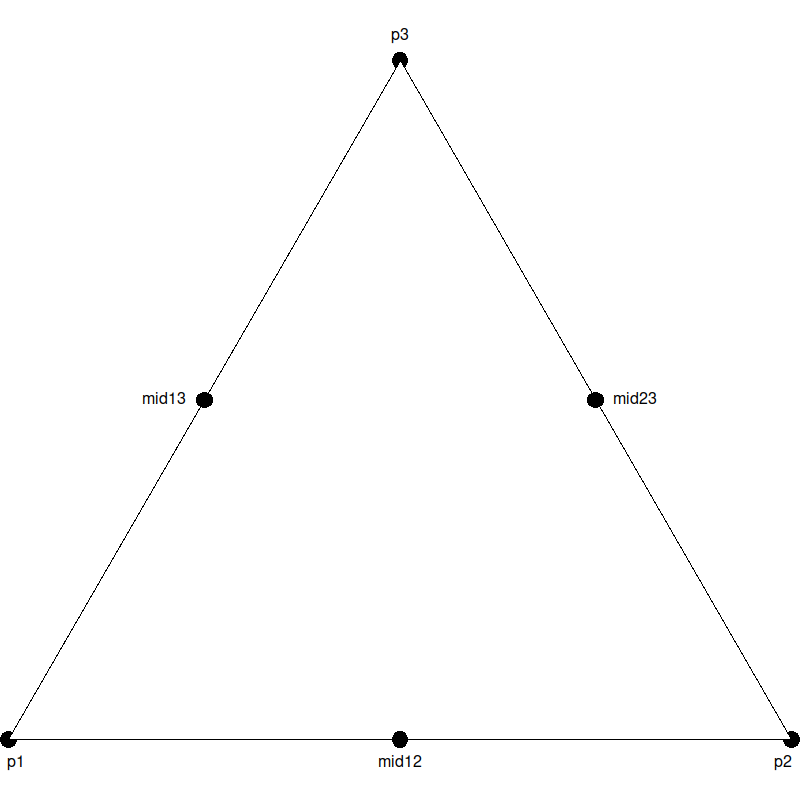

These points can be used to divide the large triangle into smaller triangles:

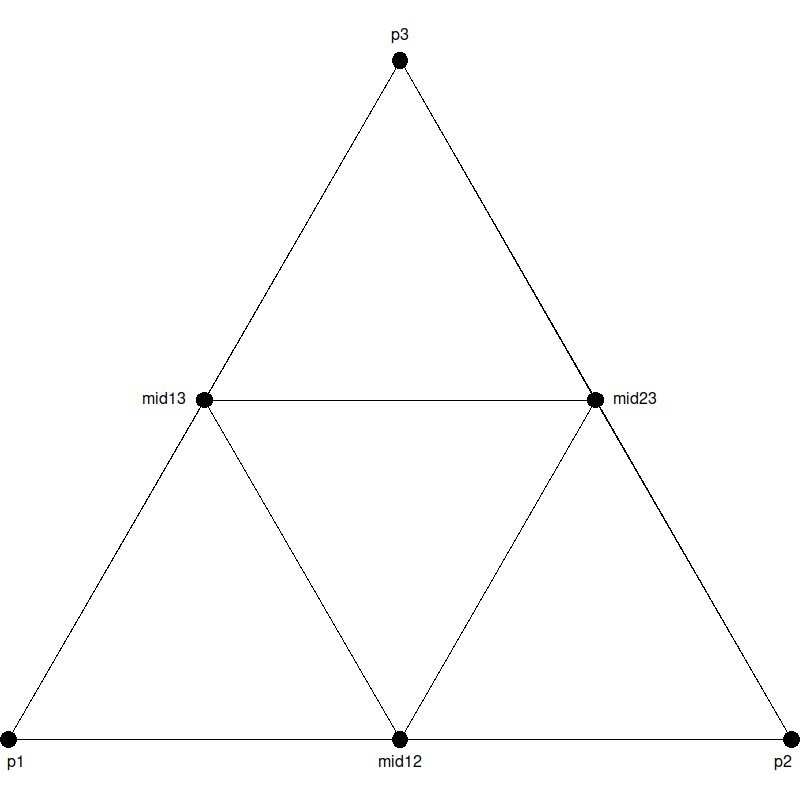
To create our pattern, we must recursively draw our pattern, for levels-1 levels, in each of the three corner triangles (but not the inverted triangle in the center). For example, your first recursive call might be on the triangle shown in purple below, defined by the points p1, mid12, and mid13: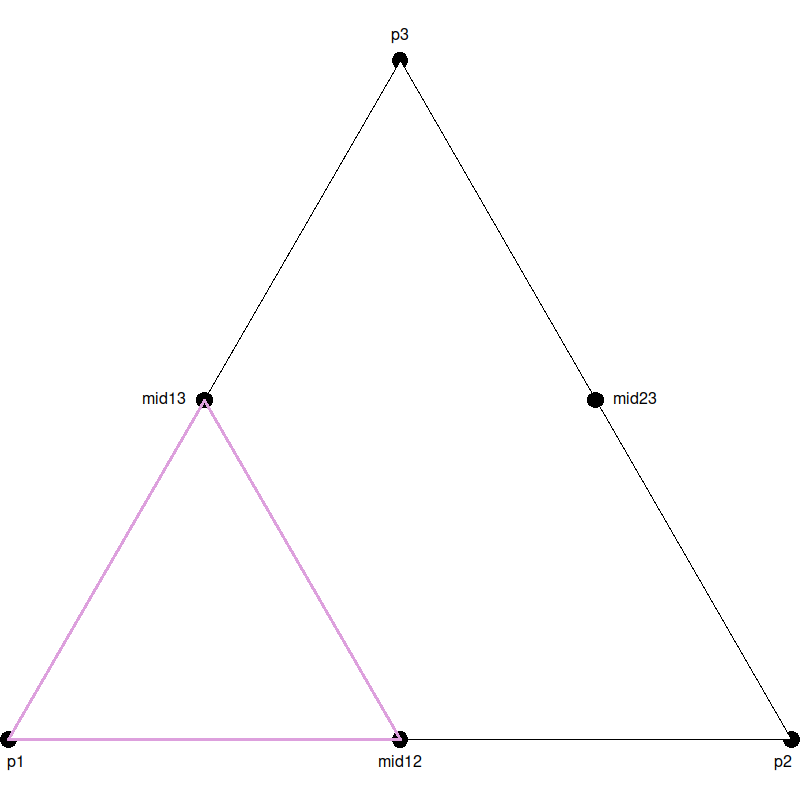

Then you want to do the same with the next two corner triangles, one given by p2, mid12, and mid23 (shown in red):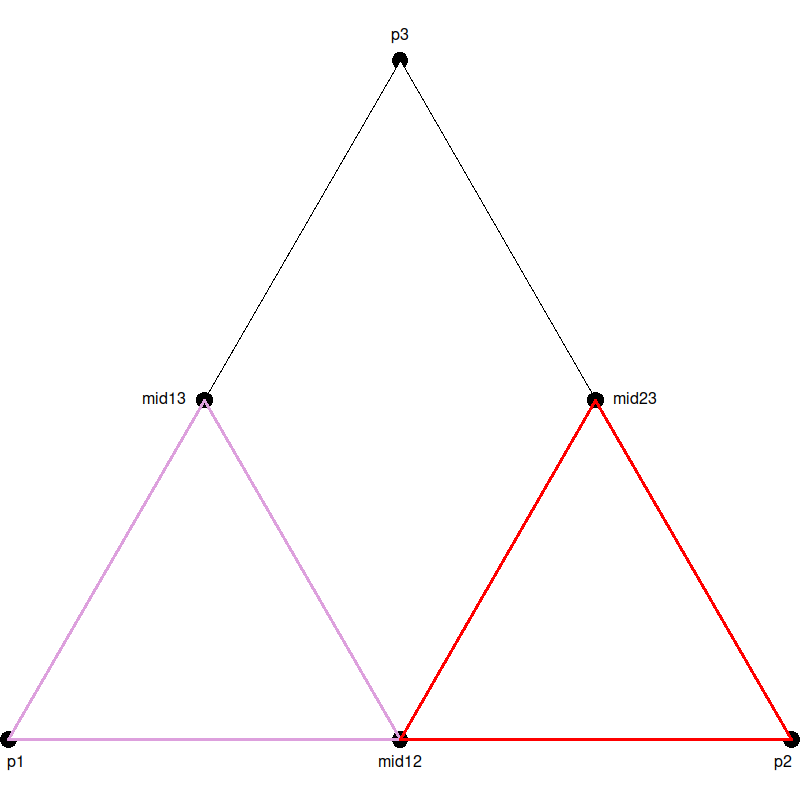

and the final one given by p3, mid13, and mid23 (shown in blue):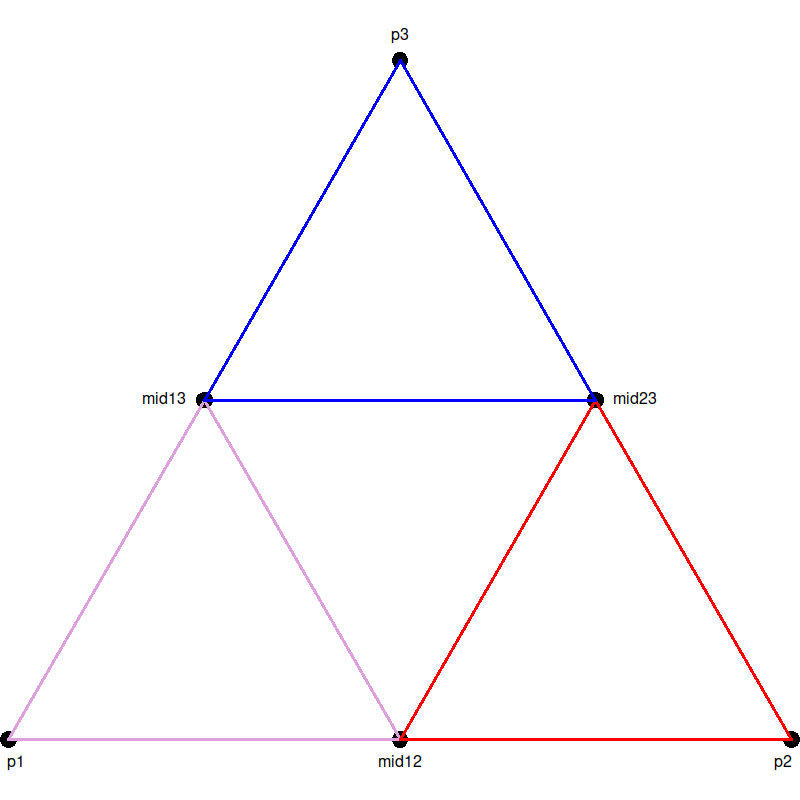

Note that you do not need to draw these triangles with these colors (we show this only for illustration purposes). Instead, your program should recursively draw our pattern, for levels-1 levels, in each of these corner triangles. With only one level of recursion (levels == 1), the result will look like this:

The pattern for one level

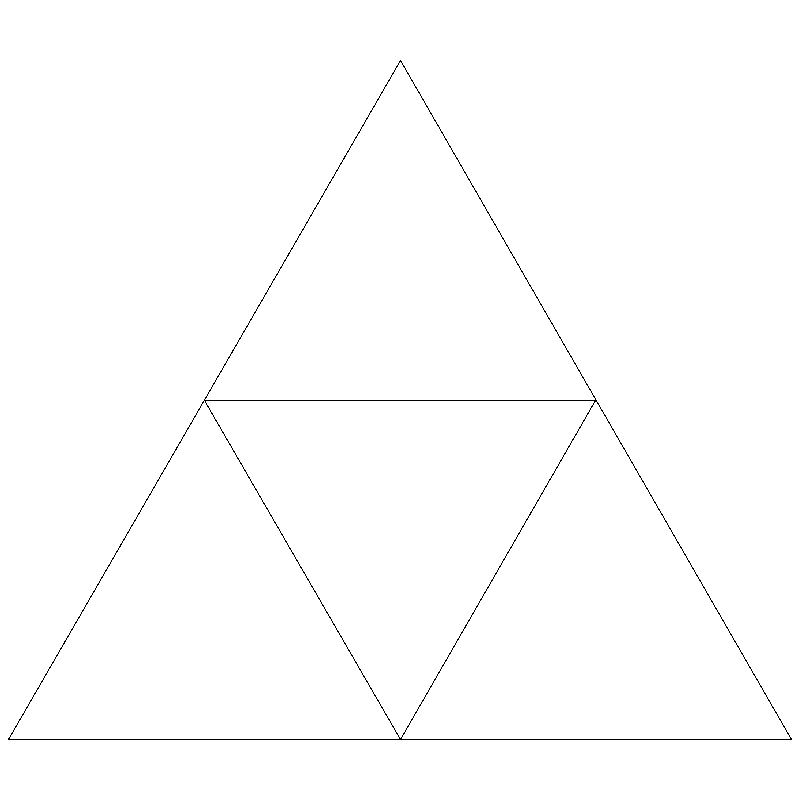
Modify the code in main to test your function with different levels. Start by making sure your program simply produces a single triangle when levels is 0 (this will help establish your base case). Then, try to make sure your drawing looks like the above when levels is 1 (this should help you get started on the recursive case). Then, test for larger levels and make sure your drawing matches the examples below. Think about your base case and make sure your recursive calls decrease the number of levels by one.

You may use whatever colors you like in your drawing. Using a simple black outline when drawing the triangle, the result should be the following for higher levels:

Our recursive pattern with 0 levels drawn

Figure 1. 0 Levels

Our recursive pattern with 1 level drawn

Figure 2. 1 Level

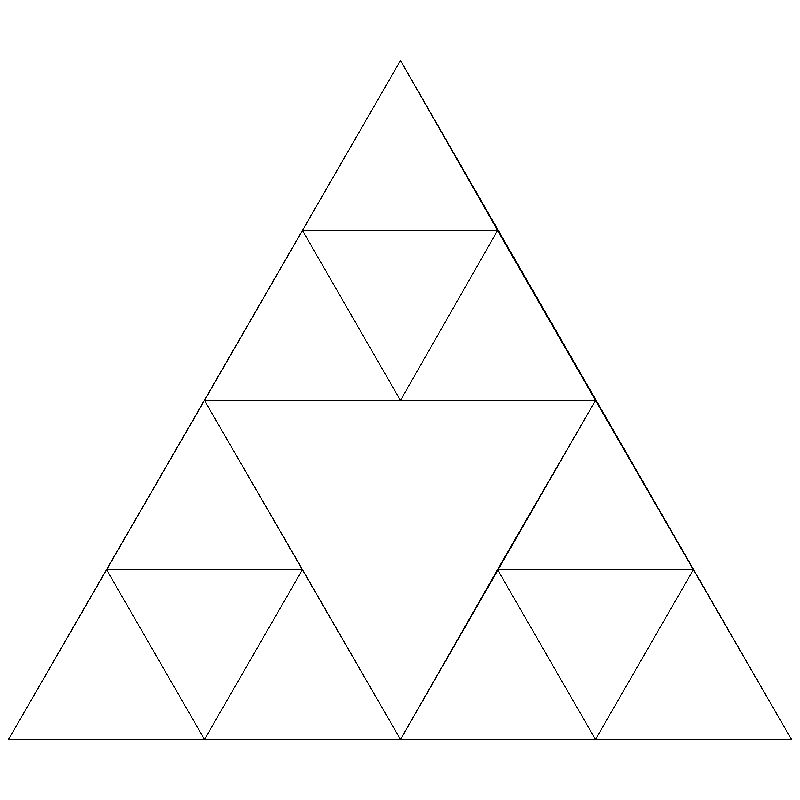
Our recursive pattern with 2 levels drawn

Figure 3. 2 Levels

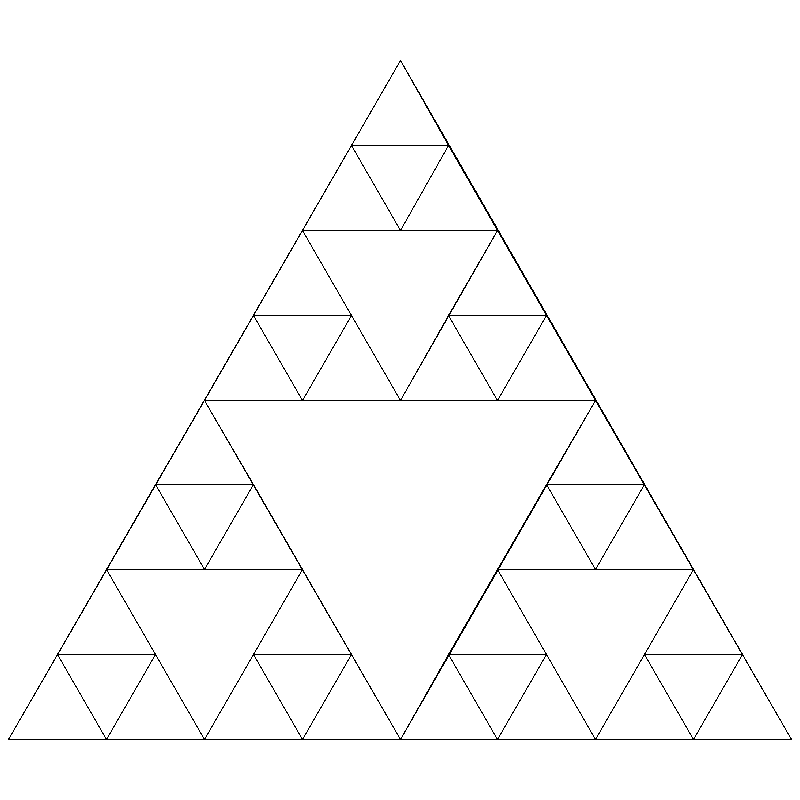
Our recursive pattern with 3 levels drawn

Figure 4. 3 Levels

Our recursive pattern with 4 levels drawn

Figure 5. 4 Levels

Our recursive pattern with 5 levels drawn

Figure 6. 5 Levels

Our recursive pattern with 6 levels drawn

Figure 7. 6 Levels

Our recursive pattern with 7 levels drawn

Figure 8. 7 Levels

Figure 9. 8 Levels

You may notice this pattern looks familiar. As we increase the number of levels, the pattern starts to look like the Sierpinski triangle, which arose from our random drawing in lab 6. We’ve created the same pattern, except now we’re doing it with recursion!

Requirements

The code you submit for labs is expected to follow good style practices, and to meet one of the course standards, you’ll need to demonstrate good style on six or more of the lab assignments across the semester. To meet the good style expectations, you should:

Write a comment that describes the program as a whole using a comment at the top of the file.
All programs should have a main() function.
Use descriptive variable names.
Write code with readable line length, avoiding writing any lines of code that exceed 80 columns.
Add comments to explain complex code segments (as applicable).
Write a comment for each function (except main) that describes its purpose, parameters and return value.

In addition, you’ll need to demonstrate good top-down design practices on two or more lab assignments across the semester. To meet the top-down design expectations, you should:

Have a main() function that serves as an outline for your program.
Your main() function should call other functions that implement subtasks.
The functions that are called by main() should be well-named and have good comments explaining their purpose, parameters (including their types), and return value (including its type).

For EACH QUESTION in the stack-diagram portion of the lab, you should meet the following requirements:

Draw the correct stack diagram.
Show the base case and recursive case.
Show the final output of the program.

For EACH PROGRAM in the function-writing portion of the lab, you should meet the following requirements:

Your function should contain a non-recursive base case.
Your function should make one or more recursive calls on a smaller version of the problem.
Your function should correctly solve the problem.
To test your solution, your main function should make at least three calls to the recursive function.

Optional

For the triangle recursion, try using the sleep() function (import it at the top of your program with from time import sleep) to add a delay between drawing triangles, so you can visualize the recursion.
For the triangle recursion, try playing around with different colors. Notice that, in addition to the three corner triangles, there is one (inverted) triangle in the middle. We should not do any recursive calls with this middle triangle, but we can separately fill it in with a color of our choosing. You can also try changing colors depending on the current level.
For the triangle recursion, try adding functionality to your main to allow the user to click to specify the three points for the initial (outermost) triangle.
Write a function get_number(n) which performs input validation using recursion. The function gets a positive integer no larger than n from the user; if the user enters an invalid input, print a message saying so and prompts again. We’ve accomplished this before using loops, but now try it using recursion.
Binary search: We saw binary search as an iterative algorithm, using a while loop. But we can also implement it recursively. Write a function binary_search(item, lst, low, high) which performs a binary search to find the index of item in the list lst between the indexes low and high.

Answer the Questionnaire

After each lab, please complete the short Google Forms questionnaire. Please select the right lab number (Lab 10) from the dropdown menu on the first question.

Once you’re done with that, you should run handin21 again.

Submitting lab assignments

Remember to run handin21 to turn in your lab files! You may run handin21 as many times as you want. Each time it will turn in any new work. We recommend running handin21 after you complete each program or after you complete significant work on any one program.

Logging out

When you’re done working in the lab, you should log out of the computer you’re using.

First quit any applications you are running, including your vscode editor, the browser and the terminal. Then click on the logout icon ( or other logout icon ) and choose "log out".

If you plan to leave the lab for just a few minutes, you do not need to log out. It is, however, a good idea to lock your machine while you are gone. You can lock your screen by clicking on the lock xlock icon. PLEASE do not leave a session locked for a long period of time. Power may go out, someone might reboot the machine, etc. You don’t want to lose any work!