CS21 Lab 10: Recursion
-
Part 1 is due on Monday, December 4 at the start of class. You may submit Part 1 on paper or you can email your professor a PDF or photograph of the the solution before the start of class. Please be sure that your paper/PDF/photograph is legible!
-
Part 2 is due on Saturday, December 2, by 11:59pm and will be turned in the "normal" way using
handin21.
Goals
The goals for this lab assignment are:
-
Practice tracing recursive functions
-
Designing recursive functions
-
Identifying base and recursive cases
1. Tracing: Stack Diagrams
The first part of this lab asks you to read four recursive functions. First, identify the base case and recursive case. Second, trace the programs, showing all program output and drawing the stack diagrams without erasing any of the stack frames after the functions end.
Example Question
Given the Python program shown below:
def fact(n):
if n <= 1:
return 1
elif
f = n * fact(n - 1)
return f
def main():
v = fact(4)
print(v)
main()Example Solution
-
Base case: when
n <= 1 -
Recursive case(s): when
n > 1 -
The final output of this program is:
Output: 24 -
The stack diagram would look like this if we didn’t erase stack frames and ran the program to completion:
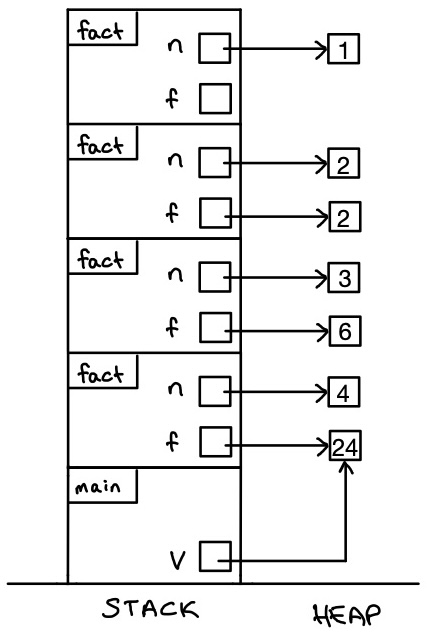
Program 1
Provide the base case, recursive case, final output, and draw the stack diagram for the program shown below.
1
2
3
4
5
6
7
8
9
10
11
12
def show(lst):
if len(lst) == 0:
print("done")
else:
print(lst[0])
show(lst[1:])
def main():
nums = [1, 5, 2, 8]
show(nums)
main()
Program 1a
Before you go on, check your understanding! What would happen if we swapped lines 5 and 6 in the program above so that it looked like the program shown below? You only need to provide the output, not the stack diagram.
1
2
3
4
5
6
7
8
9
10
11
12
def show(lst):
if len(lst) == 0:
print("done")
else:
show(lst[1:]) # these two lines were swapped
print(lst[0]) # from Program 1 shown above
def main():
nums = [1, 5, 2, 8]
show(nums)
main()
Program 2
Provide the base case, recursive case, final output, and draw the stack diagram for the program shown below.
1
2
3
4
5
6
7
8
9
10
11
12
13
def mystery(a, b):
if b == 0:
return 0
else:
p = mystery(a, b - 1)
q = a + p
return q
def main():
v = mystery(2, 4)
print(v)
main()
Program 3
Provide the base case, recursive case, final output, and draw the stack diagram for the program shown below.
1
2
3
4
5
6
7
8
9
10
11
def dub(s):
if s == "":
return s
else:
return s[0] + s[0] + dub(s[1:])
def main():
r = dub("swat")
print(r)
main()
2. Designing Recursive Functions
When designing recursive programs, the first step is to identify the base case(s) first: the simplest case where there is not a recursive call. Then move on to the recursive case(s).
2.1. Sum squares
Write a recursive function called sum_squares(lst) that takes a list of integers
as its only parameter and returns the sum of all squares of all the numbers in the the list.
You can assume that the list contains only integers. Put your solution in squares.py
in the labs/10 directory. Be sure that your solution includes a main function that tests your sum_squares function with a
few different parameter values.
Your solution must be recursive.
def sum_squares(lst):
"""
This function sums the squares of numbers in a list of integers
Args:
lst (list): a list of integers
Returns:
int: the sum of the squares of the values in the list
"""For example:
sum_squares([]) ==> 0 sum_squares([1, 3, 4, 2]) ==> 30 (since 1*1 + 3*3 + 4*4 + 2*2 = 30) sum_squares([0, 2, -4, 6]) ==> 56 (since 0*0 + 2*2 + -4*-4 + 6*6 = 56) sum_squares([5]) ==> 25
2.2. Hiding numbers
Imagine you are writing a function that hides numbers like phone numbers,
social security numbers, house numbers, etc. You will write a recursive
function called hide that replaces any digits in a string with #.
Put your solution in hide.py in the labs/10 directory. Be sure that your
solution includes a main function that tests your hide function with a
few different parameter values.
Your solution must be recursive.
For practice, you can try to write this function iteratively
(using a for loop). If you’d like to try this, call your function
hide_loop(string) in the hide.py file.
|
def hide(string):
"""
Returns a new string equal to the old string except that all of the
numbers have been replaced with the symbol #.
Args:
string (str): a string that you want to hide the numbers in
Returns:
str: the string with all numbers replaced by the symbol #
"""For example:
hide('') ==> ''
hide('SCI 256') ==> 'SCI ###'
hide('apples') ==> 'apples'
hide('555-55-5555') ==> '###-##-####'
2.3. Checking to see if all the numbers are positive
Write a function called positive(lst) that takes a list of numbers
as its only parameter and returns True if every number in the list is
positive; otherwise, the function returns False. You can assume that
the list contains only integers and/or floats. Put your solution in positive.py
in the labs/10 directory. Be sure that your solution includes a main
function that tests your positive function with a
few different parameter values.
def positive(lst):
"""
This function returns True only if every number in the list is positive.
Args:
lst (list): a list of integers and/or floats
Returns:
True if every element in the list is positive; otherwise, False
"""For example:
positive([]) ==> True positive([1, 3.14, 4, 2]) ==> True positive([1, 3.14, -4, 2]) ==> False positive([-2, -8, -9, 15]) ==> False